5.1 Короткая позиция по опциону колл
Еще раз обратимся к определению опциона колл, данному в третьей главе. Опцион колл дает владельцу право, но не обязательство, на покупку определенного количества акций (100 штук) по определенной цене (цена исполнения) при или до истечения определенного срока (дата истечения). Опционы колл — это не акции, потому что они не выпускаются корпорациями, а продаются в короткую (sold short), или выписываются (written), другими участниками рынка. Каждый раз, когда некто покупает опцион колл на акцию, торгуемую на рынке, кто-то другой его продает. На каждую длинную позицию существует короткая позиция. Что это такое — находиться в короткой позиции по колл опциону? Ключ к ответу в определении "право, но не обязательство". Владелец (то есть сторона, которая купила опцион) имеет право, но не обязательство. Тот, кто находится в длинной позиции по опциону, имеет возможность выбора: купить ему акции или нет в день или до дня истечения срока. Решающий аспект опциона колл обеспечивает особенно изогнутый профиль цены при истечении срока, как это показано на Рисунке 3.1.
Теперь представьте ситуацию, когда вы находитесь в короткой позиции на такой опцион колл (с ценой исполнения $100). Если вы находитесь в короткой позиции на этот инструмент, то вами представлено право сделать выбор владельцу опциона: взять у вас акции по $100 или нет. Вы не можете повлиять на решение обладателя опциона, но можете предположить, что он предпримет. Если цена акции выше $100 к моменту истечения срока, то он даст заявку на покупку, согласно которой вам придется предоставить ему акции по $100 за штуку. Если у вас уже нет акций, то вам потребуется приобрести их. Если цена к этому времени значительно поднялась, то вы можете понести большие убытки. Скажем, цена акции при истечении срока равна $120, тогда заявка на покупку вынудит вас купить акции по $120 и продать их владельцу опциона по $100, в результате чего убыток составит $20 за акцию. Так как для цен акций не существует верхнего предела, то нахождение в короткой позиции на опцион колл может быть весьма опасным. На практике обычно совсем не обязательно покупать акции: намного проще выкупить обратно короткий опцион и понести те же убытки. Но что, если цена акции ниже $100 к моменту срока истечения? Понятно, что владелец не станет исполнять свое право на покупку акции по $100, так как на рынке они дешевле. В такой ситуации тот, кто был в короткой позиции на опцион, выкупит его на нулевом уровне. Это — наилучшая ситуация для непокрытых продавцов (naked writers) опционов колл. Термин "непокрытый", или "голый", здесь относится к опционам колл, которые никак не хеджируются. Непокрытые продавцы берут премии за продажу опциона и рассчитывают на обесценивание опциона к сроку истечения. Вспомните одногодичный опцион колл, о котором мы говорили в третьей и четвертой главах. При цене акции $99 и сроке в один год до истечения срока опцион оценивается в $5,46. Продавец непокрытого опциона колл, выписывая один опцион, получает опционную премию $546. Если инструмент истекает без денег или обесценен, то фактически продавец может выкупить опцион за $0 и получить прибыль в $546. Это максимум того, что продавец мог бы сделать, и эта ситуация для всех продавцов непокрытого опциона одинакова. В самом лучшем случае у них остается первоначальная премия, а в худшем варианте предела убыткам нет.
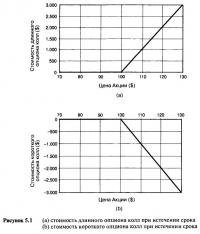
Продавцы опционов и покупатели опционов всегда находятся в противоположных ситуациях. Каждый доллар, зарабатываемый одной стороной, становится убытком другой стороны. Продавцы опционов имеют ограниченный потенциал прибыли и неограниченный потенциал убытков, в то время как покупатели опционов имеют ограниченный потенциал убытков и неограниченный потенциал прибыли. Поэтому при истечении срока профили прибылей и убытков в графическом смысле противоположны друг другу. Это означает, что все диаграммы коротких позиций на опцион являются зеркальным отображением длинных позиций. Рисунок 5.1 отражает "стоимость" рассматриваемого длинного и короткого опциона колл к сроку истечения.
Рисунок 5.1 (а) показывает стоимость длинного опциона колл, которая либо положительна, либо равна нулю, а Рисунок 5.1 (b) показывает стоимость короткого опциона колл в виде или отрицательной, или нулевой величины. При цене акции $120 длинный опцион стоит $2.000 ($20 за акцию). Это — сумма, которую владелец получает при закрытии (то есть продаже) своей длинной позиции. Итак, короткий опцион стоит $2.000, а это значит, что такую сумму продавец должен доплатить при закрытии (то есть обратной покупке) своей короткой позиции. Знак "минус" используется для того, чтобы показать, что при такой цене акции короткая позиция имеет долг величиной в $2.000. При большей цене акции долг по короткой позиции увеличивается, и об этом свидетельствует отрицательный наклон линии. Выше цены исполнения линия к истечению срока имеет наклон в $100. Для продавца опциона каждый подъем на $1 приводит к убытку в $100. Выше цены исполнения экспозиция составляет шорт 100 акций.
5.2 Чувствительности короткой позиции на опцион колл
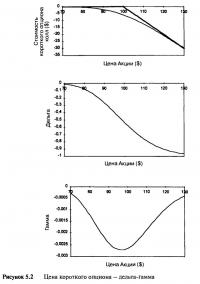
Ситуация, в которой существует короткая позиция на опцион колл до срока истечения, во всех отношениях противоположна случаю, где присутствует длинная позиция на опцион колл, поэтому очень легко выявить такие меры чувствительности, как дельта, гамма, тэта и вега. До срока истечения профиль цены (и стоимости) короткого опциона колл зеркально изогнут. Отрицательные стоимости истекающего короткого опциона колл, показанные на Рисунке 5.1, представляют общую сумму денег, требуемых для покрытия позиции, то есть величину долга, имеющегося у позиции. Рисунок 5.1 показывает общие стоимости (values) опциона, и в пересчете цен (prices) опциона на одну акцию необходимо общие стоимости разделить на 100. Также можно представить цены опциона до истечения срока из расчета за одну акцию в виде отрицательных чисел. Рисунок 5.2 показывает линии цены, дельты и гаммы портфеля, содержащего короткую позицию на одногодичный опцион колл. На реальном рынке опцион колл имеет положительную цену, а графические изображения с использованием отрицательных значений необходимы лишь для отображения изменений в стоимости короткой позиции на опцион колл. Если цена короткого опциона изменяется от -$1,00 за одну акцию до —$2,00 за одну акцию, то позиция теряет $1,00 за одну акцию. Если цена короткого опциона изменяется от —$20,00 за одну акцию до —$18,00 за одну акцию, то позиция зарабатывает $2,00 за одну акцию.
Когда цена базовой акции равна $99, наклон кривой (дельта) равен -0,5, поэтому наличие короткой позиции на один опцион колл эквивалентно экспозиции по 50 коротким акциям. Заметьте, что по мере подъема цены базовой акции наклон линии цены становится все более и более отрицательным. При очень высоких ценах акции наклон приближается к предельной величине в —1,0, поэтому нахождение в короткой позиции на опцион колл глубоко в деньгах похоже на короткую позицию в 100 акций.
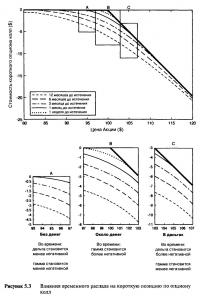
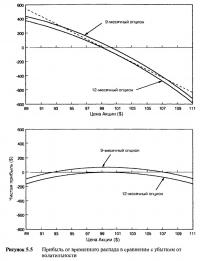
При прочих равных условиях с течением времени цена опциона падает. Иметь короткую позицию на инструмент, снижающийся в цене, считается выгодным. Временной распад (тэта) является плюсом для коротких опционных позиций, и Рисунок 5.3 показывает, как течение времени влияет на цену опциона и дельту при различных ценах акции. Опционы близко около денег переживают наибольший временной распад, а опционы далеко без денег и глубоко в деньгах — наименьший. Итак, ситуация в точности противоположна ситуации с длинным опционом колл. Короткая позиция из опциона около денег (если цена акции остается постоянной) приносит набольшую прибыль.
То, как меняется дельта во времени, также полностью противоположно тому, что происходит с длинной позицией. Дельты опционов в деньгах уменьшаются, то есть становятся все более и более отрицательными с течением времени, поэтому в пределе все опционы в деньгах, в конечном счете, ведут себя как при короткой позиции на 100 акций. Дельты опционов без денег увеличиваются, то есть становятся все менее и менее отрицательными с течением времени, поэтому в пределе все опционы без денег имеют нулевую экспозицию акции.
Гамма, или изгиб короткой позиции опциона колл есть величина отрицательная или же нулевая. Линия цены изогнута вниз, и по мере увеличения цены базового инструмента гамма является измерением скорости изменения этой наклоненной вниз линии. Около денег скорость, с которой наклон уменьшается, максимальная, поэтому в этой точке гамма наиболее отрицательна. В деньгах и без денег скорость, с которой наклон изменяется, маленькая, и в этих противоположных точках гамма, соответственно, маленькая или нулевая.
Влияния волатильности на чувствительность короткой позиции по опциону колл противоположно воздействиям, оказываемым на длинную позицию, а доказательство этого оставлено для читателя в качестве упражнения.
5.3 Простая короткая торговля волатильностью
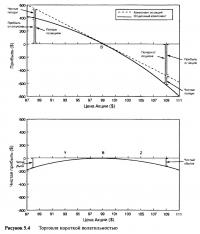
Продажа переоцененных опционов может принести хорошую прибыль, поэтому игрок короткой волатильности продает опционы в надежде на то, что получаемая им выгода покрывает больше, чем любые будущие ценовые движения. Просто продажа голых опционов чрезвычайно опасна. Короткая позиция на опционы колл эквивалентна короткой позиции по акции, лежащей в основе опциона, и если рыночная цена поднимается, то могут возникнуть большие убытки. Как и в ситуации с длинной волатильной игрой, предполагается, что игрок не имеет представления о будущем направлении движения основного инструмента, поэтому классический портфель короткой волатильности состоит из короткой позиции на опционы колл, полностью хеджируемой длинной позицией по акции. Давайте вернемся к одногодичному опциону колл. При цене акции $99 и цене опциона $5,46 дельта равна 0,5. Первоначальный портфель будет включать в себя короткую позицию на один опцион колл и длинную позицию на 50 акций. Мы в точке "В" на Рисунке 5.4, который наряду с Таблицей 5.1, показывает прибыль и убытки портфеля, где для упрощения не учитывается эффект временного распада.
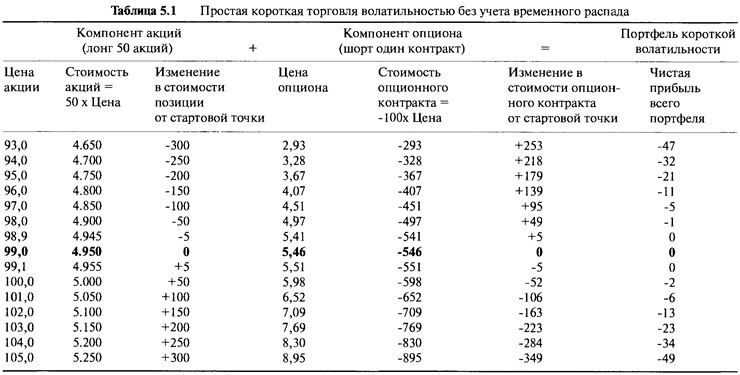
Теперь мы посмотрим, что происходит с портфелем в двух случаях. Если цена акции поднимается, то наблюдается убыток в короткой позиции и прибыль в длинной. Если цена акции падает, то прибыль будет возникать в короткой позиции, а в длинной создаваться убыток. На Рисунке 5.4 мы показали прибыль акции, а убыток изображен в виде отрицательно наклоненной линии, которая, конечно же, в действительности положительная. Иллюстрируя это таким образом, легко показать, что чистая прибыль и убыток хеджированного портфеля являются разницей между двумя линиями стоимостей, что отдельно показано на нижнем рисунке.
Малые ценовые движения акции
Если подъем цены акции маленький, то опционные убытки почти полностью ликвидируются прибылью от длинной позиции на акцию. Если цена акции упадет ненамного, то опционная прибыль почти полностью ликвидируется убытками от длинной позиции на акцию. Портфель полностью хеджирован и остается таким при небольших ценовых движениях.
Большие ценовые движения акции
Если цена акции значительно поднимается, тогда опционный компонент теряет больше, чем зарабатывается компонентом акции. Если цена акции падает значительно, тогда убыток компонента акции всегда превышает прибыль опционного компонента. Чем больше движение вверх или вниз, тем больше убыток. Вводя эту позицию, участник рынка будет надеяться на небольшие или вообще никакие движения цены акции до истечения срока, поэтому эта стратегия называется короткой торговлей волатильностью. Причина, по которой портфель всегда приносит убыток при любом направлении движения цены основного инструмента, опять-таки заключается в ценовом изгибе опциона. В коротком волатильном портфеле изгиб опциона противоположен изгибу длинного волатильного портфеля.
Рехеджирование короткого волатильного портфеля
В точке "В" на Рисунке 5.4 портфель полностью хеджирован. Экспозиция длинной позиции на 50 акций полностью ликвидирована короткой позицией на один опцион колл с дельтой 0,5. Предположим, цена акции поднимается до $105, то есть точки "Z". В точке "Z" портфель располагает нереализованным убытком в $49, и этот убыток явно будет увеличиваться, если цена основного инструмента будет повышаться. В точке "Z" дельта опциона теперь равна 0,66, и для того, чтобы быть строго рыночно-нейтральными, нам следует купить дополнительно 16 акций, чтобы пополнить длинную позицию до 66 акций. Покупка дополнительных акций переустановит позицию до дельта-нейтрального состояния. Если цена базового инструмента продолжит рост, убытки возникают снова, но уже меньшие, чем могли бы быть, если бы не были куплены дополнительные акции.
Представим, что сразу же после покупки дополнительных 16 акций по $105 цена основного инструмента начинает падать на протяжении всего обратного пути к точке "В" до $99. В точке "В" портфель опять становится несбалансированным с дельтой 0,50, поэтому мы должны теперь продать 16 акций по $99, зафиксировав убыток в 16х(105-99)=$96. Если цена продолжает падать, нам требуется сбалансировать стратегию по опциону, продав больше акций по еще более низкой цене. При цене $93 (точка "Y") дельта равна всего —0,34, поэтому 50 акциями слишком тяжело хеджировать: правильное количество здесь 34. Соответственно, нам следует продать 16 акций по $93. Если цена акции развернется снова, то для того, чтобы сохранить рыночно-нейтральное состояние, нам следует начать покупать акции на всем ее пути вверх. В точке "Z" дельта опять равна —0,50, поэтому необходимо купить 16 акций по $99, фиксируя убыток в 16х(99-93)=$96. Итак, находясь в короткой волатильной позиции и наблюдая значительные ценовые движения, всегда продаешь на низком уровне и покупаешь на высоком (selling low and buying high) — с точностью до наоборот по сравнению с длинной волатильной позицией. Процесс рехеджирования, хотя он всегда и переустанавливает позицию в рыночно-нейтральную, тем не менее всегда фиксирует убытки. Продажа на низком уровне и покупка на высоком — прямой результат того, что дельта опционной позиции двигается в обратном направлении относительно дельты основного инструмента, или проще говоря, имеет отрицательную гамму (negativegamma). Эта позиция является короткой гаммой, и данное выражение иногда используется вместо определения короткой волатильности.
Итак, зачем рехеджировать? Рассмотрим ситуацию, когда цена акции движется от точки "В" к "Z", затем опять к "В", потом к "У, к "В" и так далее, как в четвертой главе. Рехеджирование в точках "Z", "В", 'У и "В" должно включать в себя покупку акции по $ 105, продажу по $99 и так далее. Каждый кругооборот фактически фиксирует убыток в $ 192. Если цена акции всегда возвращается в точку "В" после шестидолларового колебания до "Y" или "Z" и мы не рехеджируем, тогда не возникнет никаких убытков. Вот это и есть дилемма игрока короткой волатильности. Раз цена базовой акции начала двигаться, когда же нужно рехеджировать? Мы понимаем, что если цена пройдет весь свой обратный путь до исходной точки, нам не следует, оглядываясь в прошлое, рехеджировать. Обидно покупать акции на поднимающемся рынке, зная, что придется их снова продать, если цена начнет падать. Но если вы не купите акции на пути наверх, то потенциальные убытки могут стать неограниченными. То же самое относится и к снижающимся ценам. В ситуации с падающими рыночными ценами хеджирование будет постепенно раскручено продажей акций. Если вы решите подождать надеясь, что цена акции опять поднимется, то ваши потенциальные убытки могут стать огромными.
5.4 Влияния временного распада и веги
Описание вышеуказанной стратегии наводит на вопрос: "С какой стати вообще входить в такой торг, который приносит убыток независимо от направления движения цены акции?" Ответ в том, что мы еще не видим полной картины. Для простоты изложения мы предположили, что цена опциона зависит только от цены базовой акции. В действительности же временное и рыночное восприятие волатильности тоже влияет на цену опциона. Время находится на стороне игрока короткой волатильностью. Каждый день приближает нас все ближе ко дню истечения срока, и с каждым днем некоторая часть временной стоимости покидает опцион. Рисунок 5.5 отражает более реалистичную ситуацию, включающую влияние истечения времени жизни опциона.
Влияние веги также значимо. Большинство участников рынка применяют одну и ту же модель или варианты этой модели для определения цен опционов, и единственным, наиболее важным параметром, определяющим относительную стоимость опциона, является подразумеваемая волатильность. Опцион с подразумеваемой волатильностью в 10% стоит дешевле, чем опцион с подразумеваемой волатильностью в 15%. Возможно, простая торговля, описанная выше, была вызвана предположением, что подразумеваемая волатильность в 15%, слишком высокая для рассматриваемого рынка и что, в конце концов, рынок в дальнейшем занизит цену опционов. Если это произойдет при прочих равных условиях, линия цены опциона упадет на более низкий уровень, что приведет к прибыли по этой стратегии. Следует заметить, что может произойти и обратное, а именно: рынок неожиданно осознает, что подразумеваемые волатильности слишком малы и, если ничего другого не происходит, немедленно завышает все цены опционов.
Какова бы ни была истинная причина короткой торговли, хеджирование используется для сокращения или ликвидации направленного риска. Хочет ли торговец извлечь выгоду из временного распада и/или полагает, что опционы слишком дорогие, хеджирование является попыткой ликвидировать риск, связанный со значительным подъемом цены базовой акции. Торговля принесет чистую прибыль, если влияния времени и/или снижение волатильности превысят стоимость рехеджирования.
5.5 В лучшем случае
Самый лучший исход для игрока короткой волатильностью - это когда сразу же после начала торга волатильность цены акции снижается до нуля. Как говорилось в четвертой главе, существует два типа нулевой волатильности, и простейший случай — когда цена акции остается абсолютно неизменной до наступления срока истечения. В такой ситуации максимальная прибыль будет равна потерям в размере временной стоимости опциона. На Рисунке 5.6 она представлена для различных первоначальных цен акций и называется "тип 1 максимальной прибыли".
Второй тип нулевой волатильности — тот, при котором цена акции методично движется по направлению к цене исполнения, останавливаясь в точности на цене исполнения при истечении срока. Если ценовое развитие таково, что дельта остается неизменной, то нет необходимости для рехеджирования, и не будет возникать убытков от процесса рехеджирования. Если опцион первоначально в деньгах, то цене акции придется постепенно падать по направлению к цене исполнения таким образом, чтобы влияния на дельту временем и ценой уравновешивались. В такой ситуации цена опциона будет падать весь свой путь до нуля, что приведет к прибыли, равной первоначальной стоимости опциона. Прибыль будет нейтрализована убытками хеджирования длинной позиции по акции. Если опцион первоначально без денег, тогда цена акции должна постепенно двигаться наверх по направлению к цене исполнения. В такой ситуации хеджирование длинной позиции на акции принесет прибыль, которая добавится к прибыли от опциона. Максимальная прибыль, связанная с таким типом траектории цены акции, также отражена на Рисунке 5.6 и называется "тип 2 максимальной прибыли".
Еще раз рассмотрим фиксированные контуры дельты, показанные на Рисунке 4.12. Вдоль любого контура дельта опциона постоянна. Это говорит о том, что ценовое движение акции должно выбрать очень ограниченную траекторию для того, чтобы реализовать второй тип прибыли. И помните, что это самый лучший из всех возможных вариантов — лучше быть не может. Такие ограниченные траектории цены акции, по большей части, маловероятны.
Рисунок 5.6 иллюстрирует самые лучшие варианты короткой волатильной стратегии и является зеркальным отражением Рисунка 4.16, где показаны худшие варианты длинной волатильной стратегии. Это подтверждает существование двух противоположных видов торговой стратегии. Самый лучший исход одной торговой стратегии является самым худшим в другой. Максимальная прибыль одной торговли становится максимальным убытком другой.
5.6 В худшем случае
Читателя уже не удивляет, что худший вариант для короткой волатильной стратегии соответствует лучшему варианту для длинной волатильной стратегии. Если после начала торга цена акции начинает сильно колебаться вверх и вниз, то позиция должна будет часто рехеджироваться.
Каждое движение наверх повлечет за собой покупку акции, а каждое движение вниз — ее продажу. Если такой тип поведения цены продолжается, то убытки будут постепенно расти и вполне смогут превысить прибыль, полученную вследствие временного распада. Два намного более серьезных исхода возникают при очень большом ценовом движении в одном направлении.
A. Крах рынка
Предположим, сразу же после начала торга в точке "В" цена акции внезапно падает на $60, до $39. На этом уровне опцион будет настолько далеко без денег, что будет обесценен, поэтому мы сохраним все $546 первоначальной стоимости опциона. Если мы предположим, что скорость падения была настолько велика, что не оставалось времени для рехеджирования, то убыток по 50 акциям составит 50х60=$3.000, а чистый убыток будет равен 3.000-546=$2.454. Если цена акции упадет больше, чем на $60, убыток будет еще больше.
B. Взлет рынка
Но может быть и еще хуже. Предположим, что сразу же после начала торга цена акции внезапно поднялась на $60, до $ 159. На этом уровне опцион будет настолько глубоко в деньгах, что будет оценен по внутренней стоимости, а именно в $59, в результате чего убыток составит 100х(59-5,64)=$5.336. Прибыль подлинной позиции будет 50х60=$3.000, вследствие чего чистый убыток составит 5.336-3.000=$2.336. Если бы цена акции поднялась больше, чем на $60, возник бы еще больший убыток. Теоретически не существует верхнего ограничения для цены акции, поэтому возможные убытки неограничены.
Исходя из изложенного, игра с короткой волатильностью является стратегией, с помощью которой мы заранее можем посчитать возможную максимальную прибыль, но никак не объем потерь. У этой стратегии — ограниченный потенциал прибыли и неограниченный потенциал убытков, поэтому использовать ее нужно с огромной осторожностью.
5.7 Сравнение длинной и короткой волатильности. Примеры моделирования
Можно рассматривать всех участников опционного рынка с точки зрения их нахождения в длинной или короткой позиции по волатильности. Абсолютно точно, что для каждой длинной опционной позиции существует соответствующая короткая опционная позиция. Однако необязательно все озабочены нахождением в дельта-нейтральном положении. Многие, находясь в длинной позиции на опцион колл, могут спекулировать на значительном повышении цены на базовую акцию, другие же, находясь в короткой позиции на опционы колл, могут использовать их в связке с длинными позициями на базовые акции. Интересно предположить, просто в качестве упражнения, что все открытые опционные позиции принадлежат двум группам людей: одна из них держит дельта-нейтральный портфель длинной волатильности, а другая держит дельта-нейтральный портфель короткой волатильности. Если обе группы согласны с одной и той же ценовой моделью, тогда они находятся в совершенно противоположных позициях. При сроке истечения, равном одному году, и цене акции $99 (точка "В" на Рисунке 5.4), одна группа будет иметь длинную позицию на опционы колл и короткую на 50 акций против опциона, а другая группа будет иметь короткую позицию на те же самые опционы и длинную позицию на то же количество акций. Очевидно, одна сторона полагает, что опцион стоит дешево, а другая, что он дорогой. Время покажет, кто прав.
Если цена акции поднимается до точки "Z", то оба портфеля теряют сбалансированность, но в противоположных направлениях. Игрок длинной волатильностью начинает располагать на рынке длинной позицией, а игрок короткой волатильностью — короткой. Ради упрощения давайте предположим, что оба имеют одинаковую стратегию по рехеджированию. В точке "Z" одна сторона продаст 16 акций, а другая купит 16 акций. Можно рассматривать обоих игроков как обменивающихся акциями на новом, более высоком уровне цены в $105. С течением времени, а также по мере повышения и понижения цены, акции будут переходить от одного игрока к другому. Каждый раз при сделке одна сторона будет получать прибыль, а другая терпеть убытки. Каждый проходящий день будет приносить вследствие временного распада одной стороне убыток, а другой — прибыль. К наступлению срока истечения прибыль (убытки) одной стороны будут в точности совпадать с убытками (прибылью) другой стороны. Итак, кто же выиграет, а кто проиграет? Это зависит от действительной волатильности акции, которая будет наблюдаться от начального момента до истечения срока. В вышеприведенном примере первоначальная стоимость $5,46 подразумевает волатильность в 15%. Если в действительности последующая волатильность будет выше 15%, то игрок длинной волатильностью обыграет игрока короткой волатильностью. Если действительная волатильность будет ниже, то произойдет обратное. А если действительная волатильность будет равна 15%, обе стороны будут на уровне безубыточности, так как и та и другая вошли в рынок, как оказалось, по справедливой стоимости.
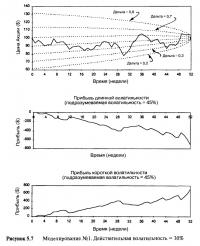
Это значит, что можно вернуться к моделям, показанным на Рисунках 4.13-4.16, и посмотреть на них с другой точки зрения. На каждом из графиков верхний рисунок показывает смоделированную траекторию цены акции, наложенную на контуры дельты. Вспомните, в этих моделированиях торговое правило заключалось в том, что каждый раз при изменении дельты на 0,10 единиц происходит рехеджирование. Поэтому каждый раз, когда траектория цены пересекает контурную линию, происходит сделка. Мы можем использовать те же моделирования цен акции для демонстрации короткой волатильной торговли. Если мы рассмотрим вышеприведенный пример, в котором все делятся на две группы игроков, то каждый раз при пересечении контура обе стороны обменивается друг с другом акциями. Прибыль одного игрока становится убытком для другого, поэтому прибыль от короткой волатильной сделки является зеркальным отображением прибыли, указанной на нижних рисунках. Следовательно, траектории цены, показанные на Рисунках 4.13 и 4.14, генерируют убытки короткой волатильной игры, а траектории на Рисунке 4.16 — прибыль.
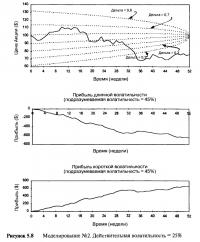
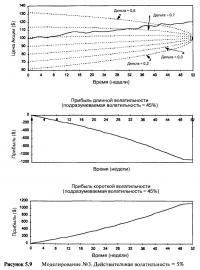
Вспомните, что во всех трех примерах первоначальная подразумеваемая волатильность опционов относительно низкая — 15%. Рисунки 5.7-5.9 показывают прибыль, возникающую при абсолютно тех же самых ценовых рядах, но при первоначально более дорого оцененном опционе в $17.22 и подразумеваемой волатильностью в 45%.
Обратите внимание, что контуры дельты на Рисунках 5.7-5.9 немного отличаются от контуров на Рисунках 4.13-4.16. Это потому, что в последних примерах мы предположили, что опцион оценивается все время так, как если бы подразумеваемая волатильность составляет 45%, а не 15%. Это дополнительная проблема для игрока с волатильностью. Чтобы оставаться строго рыночно-нейтральным, необходимо точно рассчитывать дельту. Если мы используем различные волатильности в модели, то получаем не только отличающиеся цены, но и разные дельты. При сроке в один год до истечения и цене акции $99 уровень волатильности 15% дает значение дельты 0,50, в то время как при волатильности 45% дельта 0,58. Что правильнее? Мы вернемся к этому вопросу в седьмой главе.