Изложение и опровержение английской теории ренты

Содержание:

• 350. «Рента равна разнице дохода от земли, производящей ренту, и дохода от наихудших из обрабатываемых земель.»
• 351. «Рента является также разницей в доходе, существующей между каким-либо капиталом и капиталом, применяемым при наименее благоприятных обстоятельствах».
• 352. Геометрическое выражение теории: площади чистого продукта на разных землях.
• 353. Площади чистого продукта на тех же самых землях.
• 354. Бесконечно малый характер: кривые чистого продукта и нормы прибыли в единицах продукта.
• 355. Алгебраическое выражение: функции чистого продукта и нормы прибыли.
• 356. Необходимо обсудить теорию в математической форме.
• 357. «Арендная плата (рента) — это избыток чистого продукта над процентом». Состав чистого продукта. Состав применяемого капитала.
• 358. Поправка к теории: «Арендная плата (рента) — это избыток совокупного продукта в единицах продукта над заработной платой и процентом».
• 359. Утверждая, что совокупный продукт в единицах продукта есть непропорционально возрастающая функция от применяемого капитала в денежном товаре, английская доктрина безосновательно предполагает определенными и постоянными цены личных и движимых услуг.
• 360. Данная гипотеза влечет за собой гипотезу о растущей дороговизне продуктов.
• 361. Она пригодна только для определения арендной платы в данный момент времени.
• 362. Она безосновательно предполагает, кроме того, участие одной только земельной услуги в производстве продукта, а в целом прибегает — для определения цен на земельные услуги — к рассмотрению предельных производительностей, что должно использоваться для определения земельных коэффициентов производства.

350. Теория ренты и арендной платы английской школы впервые выдвинута, как кажется, доктором Андерсоном в конце прошлого века, заново изложена в начале нашего сэром Эдвардом Вестом и Мальтусом, затем популяризировалась, главным образом, Рикардо, имя которого она носит, уточнялась Джеймсом Миллем, Мак-Куллохом, была воспроизведена Джоном Стюартом Миллем и еще в наши дни исповедуется почти всеми английскими экономистами. Вот как ее представляет Рикардо:


«Предположим, что участки №№ 1, 2 и 3 дают при равных затратах капитала и труда чистый продукт в 100, 90 и 80 квартеров хлеба. В новой стране, где плодородная земля имеется в изобилии сравнительно с населением и где поэтому необходимо возделывать только №1, весь чистый продукт будет принадлежать земледельцу и составит прибыль на вкладываемый (авансируемый) им капитал. Когда население увеличится настолько, что необходимо будет возделывать №2, с которого, за вычетом содержания рабочих, получается только 90 квартеров, то №1 начнет давать ренту. Иначе существовали бы две нормы прибыли на земледельческий капитал или же 10 квартеров (или стоимость 10 квартеров) должны были быть вычтены из продукта №1 для какой-нибудь иной цели. Возделывал ли землевладелец или какое-либо другое лицо участок №1, эти 10 квартеров все равно составят ренту, потому что тот, кто обрабатывал №2, получит одинаковый результат от своего капитала, обрабатывая № 1 и платя 10 квартеров ренты или же обрабатывая по-прежнему №2, не платя никакой ренты. Точно таким же образом можно показать, что, когда приступают к обработке №3, рента с №2 должна равняться 10 квартерам, или стоимости 10 квартеров, а рента с №1 поднимется до 20 квартеров, потому что тот, кто обрабатывал №3, будет иметь одинаковую прибыль, уплачивает ли он 20 квартеров ренты за №1, 10 квартеров ренты за №2 или же возделывает №3, не платя никакой ренты»^*.

Это — первая часть доказательства, которое Дж. С. Милль сформулировал в виде теоремы: рента равна разнице дохода от земли, производящей ренту, и дохода от наихудших из обрабатываемых земель.^** («... рента, которую принесет любой участок земли, есть положительная разница между полученным с этого участка продуктом и тем доходом, который принес бы тот же самый капитал, будь он использован на возделывание самой худшей из обрабатываемых земель». — том II, с. 155). Но Рикардо сразу же дополняет свою теорию следующим образом.

351. «Случается часто, в действительности, это обычное явление, что еще до перехода к обработке №№ 2, 3, 4 или 5 или худших земель капитал может быть более производительно затрачен на тех участках, которые уже обрабатываются. Может, например, оказаться, что при удвоении первоначального капитала, затраченного на №1, продукт хотя и не удвоится, не увеличится на 100 квартеров, но все же возрастет на 85 квартеров, это количество будет превышать то, которое было бы получено при приложении такого же капитала к земле №3.


В подобных случаях капитал будет предпочтительно прилагаться к старой земле и также доставит ренту, потому что рента всегда является разницей в продукте, полученном посредством приложения двух одинаковых количеств капитала и труда. Если при помощи капитала в 1 тыс. ф. ст. арендатор получает 100 квартеров пшеницы с арендуемой им земли и если, употребив второй капитал в 1 тыс. ф. ст., он получит еще 85, то владелец земли сможет по истечении срока аренды обязать его платить добавочную ренту в 15 квартеров или эквивалент их стоимости, ибо существование двух различных норм прибыли невозможно. Если арендатор примирится с уменьшением на 15 квартеров дохода со своей второй тысячи, то это потому, что для нее нельзя отыскать более прибыльного помещения. Такова была бы общая норма прибыли, и если бы первый арендатор отказался, то нашелся бы кто-нибудь другой, согласный отдать весь излишек прибыли сверх этой нормы владельцу земли, с которой он его получит.

В этом примере, как и в первом, последний вложенный в землю капитал не дает никакой ренты. За большую производительную силу первой тысячи ф. ст. платится продуктами квартеров в качестве ренты, за приложение второй тысячи ф. ст. не платится никакой ренты. Если к той же земле будет приложена третья тысяча ф. ст. с выручкой в 75 квартеров, то со второй тысячи будет взиматься рента, равная разности между продуктами второй и третьей тысячи, т.е. 10 квартерам, и в то же самое время рента с первой тысячи поднимется с 15 до 25 квартеров; последняя же тысяча не будет вовсе давать никакой ренты».^***

Такова вторая часть доказательства Рикардо, также сформулированная Дж. С. Миллем в виде второй теоремы: рента является также разницей в доходе, существующей между каким-либо капиталом и капиталом, применяемым при наименее благоприятных обстоятельствах.^****

352. Эта теория есть теория математическая, которую следует выражать и обсуждать математически.

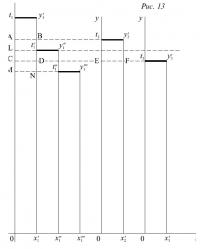
Итак, пусть даны две оси координат: горизонтальная ось Оx (рис.13) и три вертикальные оси Оу. Нанесем на горизонтальную ось из точек О отрезки Оx'₁, Оx'₂, Оx'₃, соответствующие равным объемам капитала, применяемым соответственно на участках №№ 1, 2 и 3 — объемам, по поводу которых в первой части своего доказательства Рикардо ясно не говорит, ни как они оцениваются, ни какова их стоимость, но во второй части доказательства, напротив, он вполне определенно предполагает, что они оцениваются в денежном товаре и имеют стоимость в 1000 ф. ст. А на вертикальные оси из точек О нанесем отрезки Оt₁, Оt₂, Оt₃ таким образом, чтобы, взяв эти отрезки в качестве высот, а отрезки Оx'₁, Оx'₂, Оx'₃ в качестве оснований, мы построили прямоугольники Оt₁y'₁x₁, Оt₂y'₂x₂, Оt₃y'₃x₃, площади которых количественно соответствуют чистому продукту участков №№ 1, 2 и 3, чистому продукту, который, по предположению Рикардо, оценивается в денежном товаре и составляет соответственно 100, 90 и 80 квартеров. Если это так, то первая часть доказательства означает, что — поскольку не может быть двух разных норм сельскохозяйственной прибыли — когда надо будет возделывать участок № 2, надо будет заплатить за аренду участка №1 ренту, представленную разницей двух первых прямоугольников, т.е. площадью At₁y'₁B, соответствующую 10 квартерам; а когда надо будет культивировать участок № 3, надо будет заплатить за аренду участка №1 плату, представленную разницей первого и третьего прямоугольников, т.е. площадью Ct₁y'₁D, соответствующей 20 квартерам, и за аренду участка № 2 плату, равную разнице второго и третьего прямоугольников, т.е. площадью Et₂y'₂F, соответствующую 10 квартерам, при этом за аренду участка №3 не платится никакой ренты.

353. Теперь на горизонтальную ось также нанесем из точки O в продолжение отрезка Ox1 отрезки x'₁x''₁, x''₁x'''₁, соответствующие объемам капитала в 1000 ф. ст. , применяемым последовательно на участке №1. А на параллельные вертикальной оси прямые x'₁y'₁, x''₁y''₁, проходящие через точки x'₁x''₁, нанесем из этих точек отрезки x'₁t'₁, x''₁t''₁ таким образом, чтобы, построив прямоугольники, имеющие эти отрезки в качестве высот, а отрезки x'₁x''₁, x''₁x'''₁ в качестве оснований, мы получили площади этих прямоугольников x'₁t'₁y''₁x''₁, x''₁t''₁y'''₁x'''₁ равные количествам, соответствующим чистому продукту от последовательных вложений капитала в 1000 ф. ст., осуществляемых на участке №1, чистому продукту, который по-прежнему оценивается в денежном товаре и составляет соответственно 85 и 75 квартеров. Если это так, то вторая часть доказательства означает, что — поскольку не может быть двух разных норм прибыли — когда нужно будет осуществить в участок №1 второе вложение капитала в 1000 ф. ст. , вложение, которое будет сделано после того как участок №2 уже введен в оборот, и до того, как вводится в оборот участок №3, то надо будет выплатить в расчете на первый применяемый капитал в 1000 ф. ст. ренту, представленную разницей двух прямоугольников Ot₁y'₁x'₁ и x'₁t'₁y''₁x''₁, т.е. площадью Lt₁y'₁t'₁, соответствующую 15 квартерам; а когда надо будет осуществить в тот же участок №1 третье вложение капитала в 1000 ф. ст. , то надо будет выплатить в расчете на первое вложение капитала в 1000 ф. ст. ренту, представленную разницей двух прямоугольников Ot₁y'₁x'₁ и x''₁t''₁y'''₁x'''₁, т.е. площадью Mt₁y'₁N, соответствующую 25 квартерам, и в расчете на второе вложение капитала ренту, представленную разницей двух прямоугольников x'₁t'₁y''₁x''₁ и x''₁t''₁y'''₁x'''₁, т.е. площадью Nt'₁y''₁t''₁, соответствующую 10 квартерам, таким образом, что в конечном счете за аренду участка № 1 будет выплачена рента, представленная суммой двух площадей Mt₁y'₁N и Nt'₁y''₁t''₁, т.е. площадью Mt₁y'₁t'₁y''₁t''₁, которая соответствует 35 квартерам.


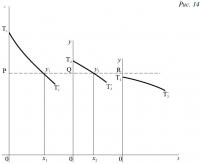
354. После того как теория выражена в математической форме, один момент сразу же становится очевидным: то, что Рикардо говорит о равных вложениях капитала, осуществляемых последовательно либо на разных землях, либо на одной и той же, должно быть сказано — независимо от того, справедливо это или нет — не только о вложениях в 1000 ф. ст., но также и о вложениях в 100 ф. ст., в 10 ф. ст., в 1 фунт; короче, дело в том, что, если норма выхода продукции является для каждого участка убывающей функцией от применяемого капитала, то нет никакой причины не предполагать, что, когда применяемый капитал увеличивается на бесконечно малое количество, то норма выхода продукции должна уменьшаться на бесконечно малое количество. Разумеется, может быть и иначе; но до тех пор, пока нам не показали — путем рассуждения или на опыте — что это последнее является общим случаем, мы вправе теоретически рассуждать на базе первого. Таким образом, дискретные кривые, такие как кривая t₁y'₁t'₁y''₁t''₁y'''₁..., чтобы выразить факт убывания, о котором идет речь, следует заменить на непрерывные кривые T₁T'₁, T₂T'₂, T₃T'₃. (рис. 14), построенные таким образом, чтобы, когда капитал, применяемый на участках №№ 1, 2. представлен длинами отрезков Ox₁, Ox₂..., чистый продукт (в единицах продукта) был представлен площадями OT₁y₁x₁, OT₂y₂x₂. Тогда учет того соображения, что не может быть двух норм прибыли сельскохозяйственного капитала, потребует, чтобы площади прямоугольников OPy₁x₁, OQy₂x₂, представляющие в единицах продукта данные прибыли на участках №№ 1, 2..., были пропорциональны их основаниям Ox₁, Ox₂..., иначе говоря, чтобы высоты этих прямоугольников, x₁y₁, x₂y₂ представляющие в единицах продукта норму прибыли, т.е. норму выхода продукции, были равны. И, следовательно, части площадей PT₁y₁, QT₂y₂..., находящиеся выше горизонтальной линии PQR, будут выражать в единицах продукта рентные платежи за участки №№ 1, 2, а участок № 3 не дает ренты, если, как предполагается на нашем рисунке, горизонтальная линия PQR не пересекает кривую T₃T'₃.

355. Пусть n₁, n₂, n₃... — соответствующие числа в гектарах участков №№ 1, 2, 3. И пусть в расчете на гектар: h₁, h₂, h₃... — излишки общего числа единиц продукта над числом, необходимым для выплаты заработной платы, x₁, x₂, x₃... — применяемые капиталы, выраженные в денежном товаре, t — норма процента, выраженная в денежном товаре; тогда ренты r₁, r₂, r₃..., выраженные аналогичным образом, будут даны уравнениями



Чистый продукт и применяемые капиталы связаны отношениями


а норма процента и применяемые капиталы — отношениями


причем эти два вида отношений представлены одновременно кривыми, такими, как T₁T'₁, T₂T'₂, T₃T'₃..., в которых переменная x соответствует абсциссам, а функция t — ординатам и функция h — площадям.

Внимательное рассмотрение вышеуказанных уравнений позволяет выяснить, что для m номеров участков имеется 3m+1 неизвестных и только 3m уравнений. Нужно еще одно уравнение. Придерживаясь возможно более верного толкования теории Рикардо и сообразуясь с аналогичными прецедентами (242, 248), мы можем сформулировать следующее уравнение:


Согласно Рикардо, как представляется, в обществе имеется некоторый постоянно возрастающий капитал, с помощью которого можно получать постоянно возрастающее, хотя и не пропорционально, количество продуктов с тем, чтобы можно было кормить постоянно возрастающее население. В данный момент времени этот капитал определен; мы обозначаем его через X и распределяем его среди земельных участков разного вида таким образом, чтобы норма выхода продукции была одной и той же на всех участках.

Уравнения [3], если предположить их решенными относительно x, принимают форму


тогда t дается уравнением [4], измененным таким образом


После того как t найдено, x₁, x₂, x₃... находятся с помощью видоизмененных уравнений [3]. Земли, для которых имеем F'(0)<t, не обрабатываются; обрабатываются только земли, для которых F'(0)>t. После того как найдены x₁, x₂, x₃..., находим h₁, h₂, h₃... с помощью уравнений [2]. И тогда r₁, r₂, r₃... определяются посредством уравнений [1]. Таким образом, арендные платы зависят, в конечном счете, от капитала страны и определяются отдельно от заработных плат и процента, а также от цены продуктов. Такова суть английской теории ренты.

356. Необходимость придать рассуждению Рикардо характер анализа бесконечно малых величин ощущается настолько сильно, что некоторые авторы почувствовали ее, не отказываясь от обычного языка, так что окончательная форма, в которую мы облекли его, является вполне настоящей формой английской теории ренты. Вот почему мы будем ее придерживаться в ходе обсуждения, не останавливаясь на недостатках изложения или дедукции, связанных у Рикардо и Милля с использованием рудиментарной формы, не показывая, например, как первая теорема Милля, предполагающая в основном, что наихудшие из обрабатываемых земель не дают арендной платы, недостаточно обоснована сама по себе и, впрочем, формально противоречит второй. Действительно, эта ошибка исчезает в математической теории; простое рассмотрение рисунка показывает, что наихудшие из обрабатываемых земель дают ренту, по крайней мере в общем случае помимо исключительного случая, когда дискретная кривая продукта пересекается как раз в исходной точке с горизонтальной линией нормы выхода продукции.

357. Итак, вернемся к общему уравнению


и пусть, согласно нашим обозначениям, (В) — рассматриваемый продукт, p_b — его цена, (Т) — вид земли, на которой его возделывают, H — общее число единиц, получаемых с гектара и, следовательно, b_t=1/H — коэффициент производства продукта (В) в производительной услуге (Т), p_t — арендная плата и i — норма чистого дохода в денежном товаре. r и t, которые являются соответственно, как мы видели, арендной платой и нормой процента, выраженными в единицах продукта, могут быть заменены на значения p_t/p_b и i/p_b в вышеприведенном уравнении, который тем самым примет вид


Пусть к тому же (P), (P'), (P'')... — виды личных капиталов, или людей, чьи услуги также входят в производство продукта (В), b_p, b_p', b_p''... — производственные коэффициенты, p_p, p_p', p_p''... — цены личных доходов, или заработные платы, P_p, P_p', P_p''... — цены личных капиталов в денежном товаре; чистый продукт в единицах продукта, h, в том виде, как его ввел Рикардо, равен


т. е., отвлекаясь от амортизации и страхования, чтобы не усложнять формулы, равен


Пусть, наконец, (K), (K'), (K'')... — виды движимых капиталов, или собственно капиталов, чьи услуги также входят в производство товара (И), b_k, b_k', b_k''...- производственные коэффициенты, p_k, p_k', p_k''... — цены движимых капиталов, или процент, P_k, P_k', P_k''...- цены движимых капиталов в денежном товаре; применяемый капитал в том виде, х, как его вводит Рикардо, равен


или, отвлекаясь от амортизации и страхования, равен


358. Итак, отметив это, мы имеем, разумеется, основание внести прежде всего поправку в уравнение, которое мы хотим обсудить, затрагивая теорию Рикардо лишь так, чтобы сделать ее максимально строгой: она состоит в том, чтобы объединить цены людей (P), (P'), (P'')... с ценами собственно капиталов (K), (K'), (K'')... и получить в члене х совокупный объем капитала, будь то капитал движимый или личный; ибо очевидно, что норма заработной платы одна, как и норма процента, и что она, кроме того, в точности равна норме процента, так что можно и должно рассуждать одновременно о единице того и другого — в теории, как это и делали некоторые английские экономисты. После того как это исправление сделано, чистый продукт h совпадает с совокупным продуктом H и применяемый капитал становится окончательно


359. Таковы будут H и х, являющиеся функцией друг друга и представленные: первое — площадями, второе — абсциссами кривых TT'. А теперь нет ничего проще узнать, является ли член H непропорционально возрастающей функцией от х, т. е., иными словами, являются ли кривые TT' убывающими. Действительно, достаточно поставить вопрос, является ли отношение


убывающим, когда х и H возрастают.

Однако является установленным на опыте фактом, что, присоединяя к земельному капиталу возрастающие количества личных и движимых услуг, нельзя получить пропорционально возрастающие количества продукта; если бы это было не так, то с одного гектара земли и даже с меньшей площади можно было бы получить — путем присоединения бесконечного количества личных и движимых услуг — бесконечное количество продуктов. Таким образом, если выражаться точно, можно сказать, как мы это делали ранее (325), что b_p, b_p', b_p''... b_k, b_k', b_k''... являются не постоянными количествами, а убывающими функциями от b_t, т. е. возрастающими функциями от H.^***** Но Рикардо и английские экономисты говорят совсем другое. Они говорят, что, осуществляя на какой-либо земле возрастающие вложения личного и движимого капитала, мы не получаем продукции в пропорционально возрастающем количестве; при этом вложения капитала, о которых они говорят, оцениваются в денежном товаре. Чтобы такое утверждение отождествить с предыдущим, необходимо предположить, что вложения, равные по количеству выражающего их денежного товара, есть также вложения, равные по количеству представляющих их личных и движимых услуг, поскольку в ином случае — и предполагая, что равным количествам денежного товара соответствуют более чем равные (большие) количества производительных услуг — ничто не помешало бы представить продукт как пропорциональный вложению капитала. Выражаясь точно, чтобы иметь возможность сказать, что H является непропорционально возрастающей функцией от x не только в данный момент времени, но и в разные моменты времени, необходимо предположить P_p, P_p', P_p''... P_k, P_k', P_k''...i, и, следовательно, p_p, p_p', p_p''... p_k, p_k', p_k''... не только как определенные в некоторый момент времени, но и как постоянные от одного момента времени к другому.

Если перечитать изложение Рикардо, то мы увидим, что это двойное предположение в неявном виде (а то и в явном) присутствует у него от начала и до конца. Разумеется, Рикардо не мог бы утверждать, что получаемый продукт зависит от применяемого капитала, каким бы образом он ни применялся, пусть даже абсурдным. Следовательно, для него вложения капитала, осуществляемые — будь то одновременно или же последовательно — на различных участках или на одном и том же, представляют собой известные определенные количества известных определенных капиталов. Эти вложения составляют всегда 1000 ф. ст.; значит, цены капиталов являются определенными и постоянными. Но, в целом, продукт зависит именно от природы и количества производительных услуг. Следовательно, надо допустить, что для Рикардо вложениям известных определенных количеств известных определенных капиталов соответствуют вложения известных определенных количеств известных определенных услуг. Вложения капиталов составляют всегда 1000 фунтов; пусть норма процента равна 5%, «вложения» услуг будут составлять всегда 50 фунтов; следовательно, цены услуг определенны и постоянны.

360. Данная гипотеза имеет серьезные последствия, на которые важно указать. Именно она привела Рикардо к тому, чтобы обосновывать существование, появление и развитие ренты фактом дороговизны продуктов. Действительно, для него именно себестоимость определяет продажную цену. С другой стороны, как мы только что видели, определенные и постоянные издержки, необходимые для получения чистого продукта, составляют 50 фунтов. Если добавить к обработке участка № 1, где 50 фунтов издержек дают 100 квартеров чистого продукта, обработку участка № 2, где 50 фунтов издержек дают 90 квартеров чистого продукта, то себестоимость и, следовательно, продажная цена поднимется с 50/100 до 50/90 фунтов. Или же если при обработке участка № 1 к исходным издержкам в 50 фунтов, дающим 100 квартеров чистого продукта, добавить другие издержки в 50 фунтов, дающие 85 квартеров чистого продукта, то себестоимость, являющаяся также продажной ценой, поднимется с 50/100 до 50/85 фунтов. В нашем математическом изложении теории Рикардо мы добавляем к издержкам на процент издержки на заработную плату, но результат тот же. Действительно, цена продуктов p_b равна отношению либо совокупных издержек на арендную плату, заработную плату и процент, p_t+xi, к валовому количеству продуктов, H, либо издержек на арендную плату, p_t, к арендной плате в единицах продукта, r, либо, наконец, издержек на заработную плату и процент, xi, к заработной плате и проценту в единицах продукта, xt, т. е., следовательно, отношению i/t. Но, ведь, отвлекаясь от изменений i, это отношение растет бесконечно в силу убывания t, что является основой теории.

Отсюда, в конечном счете, следует, что арендная плата в денежном товаре удваивается от одного момента времени к другому, во-первых, в силу увеличения числа единиц продукта, которые ей соответствуют, r, и, во-вторых, в силу увеличения цены этого продукта, p_b. Это последствие было в полной мере замечено и принято Рикардо; оно является предметом специального примечания в конце его главы «О ренте».

361. Таким образом, английская теория ренты определяет ее цену и доказывает ее прибавочную стоимость только при двойном условии: предполагая, что цены личных и движимых капиталов, норма чистого дохода и, как следствие, цены личных и движимых услуг являются определенными и постоянными. В двух следующих уроках мы увидим, что английская школа не определяет ни заработную плату, ни процент; но пока мы можем сделать ей уступку, допуская за ней такое определение. Например, мы не могли бы априорно принять ее допущение о постоянстве цен на производительные услуги. Отсюда следует, что кривые или уравнения, определяющие продукт как функцию от применяемого капитала, не имеют никакого значения в том, что касается сравнения арендной платы в разные моменты времени в связи с последовательными вложениями капитала, или в том, что касается формулирования закона изменения арендной платы в прогрессивном обществе; что они могут, самое большее, служить лишь для определения всего-навсего арендной платы в данный момент времени в связи с одновременными вложениями капитала или же для формулирования закона установления арендной платы. Только в этих пределах можно использовать кривые или уравнения, о которых идет речь. Предполагая в таком случае p_p, p_p', p_p''... p_k, p_k', p_k''... определенными, арендная плата будет определяться в единицах продукта уравнением


и в денежном товаре уравнением


Если, подставляя, что мы и предполагали сделать (358), H вместо h, мы полагаем


и, следовательно,


то мы можем поставить уравнение [5] в виде


и тогда мы ясно видим, как уравнение


или кривая TT', которая его представляет, будучи в максимально возможной мере исправленными и дополненными, дают арендную плату в единицах продукта как убывающую функцию применяемых количеств капитала или личных и движимых услуг; и уже сейчас можно задаться вопросом, почему английская школа скорее определяет арендную плату через используемые количества труда и прибыли, нежели заработную плату и процент через используемые количества ренты, и почему даже она не пытается определить цены всех производительных услуг одинаковым образом с помощью общей теории. И тем не менее, вводя это уравнение или эту кривую (которую следует принимать лишь с предшествующей оговоркой и имея ввиду еще одну более серьезную, о чем ниже), английская школа вводит с грехом пополам — в общую задачу определения цен — число уравнений, равное числу неизвестных, которыми являются арендные платы в единицах продукта. И поставленная таким образом теоретически задача решается практически через конкуренцию предпринимателей. Уточнив это, остается определить, с другой стороны, неизвестные, которыми являются заработные платы, процент и норма чистого дохода в денежном товаре. После чего норма выхода продукции будет определяться, как говорилось ранее (355), в соответствии с имеющимся количеством капитала; цена продуктов будет определяться через отношение нормы чистого дохода к норме выхода продукции, и, наконец, можно будет определить арендную плату в денежном товаре, умножая арендную плату в единицах продукта на цену продуктов. Таким манером английской школе удалось бы, следовательно, установить, что арендная плата не входит в состав издержек производства; и это последний подводный камень, который нам остается отметить, и, натолкнувшись на который, ее теория ренты окончательно рухнет.

362. Заменяя в уравнении [6] Hна 1/b_t, умножая на b_t и переставляя количество, заключенное в скобки, в левую часть, получаем:


уравнение, являющееся не чем иным, как уравнением себестоимости продукта (В) в том виде, как оно фигурирует в системе [4] наших уравнений производства (203) с тем, однако, ограничением, что, если в производство этого продукта входит несколько видов работ (P), (P'), (P'')... и прибылей (K) (K'), (K'').., то сюда входит лишь один вид ренты (T). Таким образом, английская теория ренты опирается также на гипотезу о том, что в производство продуктов всегда входит лишь один вид земельных услуг. Но эта гипотеза неточна в том, что касается как сельскохозяйственных, так и промышленных продуктов. Пшеница, служащая Рикардо примером, сюда не относится, ибо в производстве пшеницы участвует сырой материал, которым является удобрение, получаемое от скота, кормящегося на лугах, представляющих собой земли иного рода, нежели пшеничные поля. На этом основании, а также потому, что английская школа прямо не определяет ни заработную плату, ни процент, необходимо дополнить уравнение себестоимости продукта (В) следующим образом:


добавить к нему уравнение производства


и затем объединить его с другими уравнениями производства чтобы определить одновременно цены продуктов и цены производительных услуг. Рассмотрение предельной производительности, которое английская школа использует путанным и некорректным образом для определения цен земельных услуг, будет служить для определения производственных коэффициентов точно так же, как рассмотрение издержек производства, которое она использует для определения цен продуктов, будет служить для определения производимых количеств продукции^******. Итак, все, что остается, таким образом, от теории Рикардо после строгой критики — это то, что арендная плата (рента) является не элементом, а результатом цены продуктов. Однако то же самое можно сказать о заработной плате и проценте. Следовательно, арендная плата, заработная плата, процент, цены продуктов и производственные коэффициенты являются неизвестными одной и той же задачи и должны определяться все вместе, а не независимо друг от друга.

Примечания

* Рикардо. Начала. гл. II, с. 113 (по переводу Рязанова, 1908, с. 36-37).

** Дж. С. Милль. Основы. , там же, том II, кн. II, гл. XVI, § 3, с. 155.

*** Рикардо. Начала. гл. II, с. 113-114 (Рязанов — с. 37-38).

**** Дж. С. Милль. Основы. , том II, кн. II, гл. XVI, § 4 (с. 158).

***** Здесь следует опустить то обстоятельство, что производственные коэффициенты являются не только функциями от b_t и H, но и функциями по отношению друг к другу.

****** Для продукта (В), производимого двумя услугами (T) и (K), уравнения [1] и [3] предельной производительности (326) дают


Если предположить Q = Hтаким образом, чтобы T = Hb_t = 1 и K = x, то функция Q = F(T,K) становится H = F(x) , а частная производная (dF/dK) = Fy(x), тогда вышеприведенное уравнение становится


т. е. тождественным теоретическому уравнению (математической) ренты Рикардо (1902).