- 306. Обращение векселей.
- 307. Курс обмена. Курс в собственном смысле слова. Паритет, потеря, премия.
- 308. Расчеты путем трассирования и переводы векселей.
- 309. Определение курса.
- 310. Ограничения потерь или премий при вексельном обмене.
- 311, 312. Уравнение вексельных курсов.
- 313. Общее равновесие вексельных курсов.
- 314. Арбитражные сделки.
- 315, 316. Последствия арбитражных сделок.
306. Банковские билеты обращаются только внутри той страны, где они выпущены; сфера обращения переводных векселей гораздо шире. Переводные векселя на Париж и Лондон поступают из любого уголка Европы, Восточной Индии, Америки; эти тратты проходят через бесчисленное количество рук, опосредуя многочисленные и разнообразные сделки купли-продажи, прежде чем попадут в то место, где их должны оплатить. Вот почему переводные векселя имеют исключительное значение среди бумажных денег. Большие коммерческие и банковские центры — Лондон, Париж, Амстердам, Гамбург, Франкфурт, Генуя, Триест, Нью-Йорк — являются одновременно и рынками, на которых покупаются и продаются переводные векселя. В каждом из них ежедневно котируются векселя, выписанные на все остальные центры: эти котировки называются обменным (вексельным) курсом или просто курсом (change). Так, в Лондоне котируются векселя на Париж, Амстердам, Гамбург, Геную; в Париже — на Лондон, Амстердам, Франкфурт, Триест; в таких случаях, к примеру, говорят: «В Париже сегодня лондонские стоят 25.15, амстердамские 208.25, франкфуртские 210, триестские 195.50», что означает, что 1 фунт стерлингов к оплате в Лондоне покупается и продается за 25.15 франков в Париже, что 100 флоринов к оплате в Амстердаме, Франкфурте или Триесте покупаются и продаются в Париже за 208.25, 210 и 195.50 франков соответственно. Отсюда видно, что для указания обменного курса требуются две вещи: одна величина достоверная, которая подразумевается, это — 1 фунт стерлингов, 100 флоринов, и одна величина неизвестная, которая указывается, это — 208.25, 210 или 195.50 франков. Лондон, Амстердам, Франкфурт, Триест в этом примере дают нам достоверную величину, а Париж — неизвестную.
307. При определении этих курсов один элемент связан с разницей денежных единиц, а другой — с собственно курсом (курсовой разницей) . Так, один фунт стерлингов содержит столько же чистого золота, сколько его было бы в монете на 25.22 франков. Если бы, следовательно, курс Лондона в Париже составлял 25.22, то обмен осуществлялся бы по паритету: некоторая сумма к оплате золотом стоила бы одинаково что в Лондоне, что в Париже. Разница между курсом в 25.15 и паритетом в 25.22 составляет в этом случае курсовую разницу. Ситуация упрощается и курсовая разница выступает в чистом виде, когда векселя выписаны в тех же денежных единицах. Так, когда говорят, что брюссельские векселя в Париже стоят 101, а генуэзские — 95, то это означает, что 100 франков к оплате в Брюсселе покупаются в Париже за 101 франк, а 100 итальянских лир к оплате в Генуе покупаются в Париже за 95 франков. В этом случае брюссельские векселя стоят выше паритета, принося премию, а генуэзские — ниже, принося потерю.
Курс, таким образом, в общем виде есть цена на данном рынке некоторой суммы к оплате в другом месте. От каких причин зависит большая или меньшая цена суммы к оплате в другом месте на данном рынке? Этот вопрос мы и будем исследовать. Для этого рассмотрим, в каких условиях протекает торговля переводными векселями.
308. Платежи из одного места в другое осуществляются, как правило, путем передачи векселей, а не путем пересылки металлических денег. Пусть лондонский торговец X продал парижскому торговцу Y некоторые товары. В то же время парижский торговец Z продал товары лондонскому торговцу W на сумму, как мы можем предположить, равную первой. При данных условиях нет нужды, чтобы парижский торговец Y отправлял золото или серебро в Лондон для X, а лондонский торговец W высылал золото или серебро в Париж для Z. Оба этих платежа могут осуществиться без участия металлических денег, путем выставления и перевода векселя. Пусть торговец X из Лондона выставляет вексель на Y из Парижа; если W в Лондоне купит этот вексель, то X получит свои деньги, а W заплатит. Пусть W теперь переведет этот вексель в Париж для Z; теперь, как только Z погасит этот вексель у Y в Париже, то Z получит свои деньги, а Y заплатит. Таким образом оба долга будут погашены, а оба кредита возвращены.
309. Таков принцип; обратимся теперь к практике и предположим для простоты, что в городах обращается одна и та же денежная единица. Пусть разные торговцы из Брюсселя продали разным торговцам в Париже товаров на общую сумму в 101000 франков. С другой стороны, пусть разные торговцы из Парижа продали разным торговцам в Брюсселе товаров на общую сумму в 100000 франков. Из того, что было сказано выше, ясно, что нет надобности посылать 101000 франков золотом или серебром из Парижа в Брюссель, в то время как из Брюсселя будет послано 100000 франков в Париж. Пусть кредиторы из Брюсселя выставят векселя на Париж на сумму 101000 франков и продадут их в целом за 100000 франков дебиторам в Брюсселе на счет дебиторов из Парижа; или же пусть кредиторы из Парижа выставят векселя на Брюссель на сумму 100000 франков и продадут их в целом за 101000 франков дебиторам в Париже на счет дебиторов из Брюсселя; или же пусть эта операция осуществляется частично в одном и частично в другом направлении, но пропорциональными долями, так чтобы ни один дебитор, будь он в Брюсселе или Париже, не мог выгадать от покупки векселя вместо того, чтобы вексель выписывался на него. Во всяком случае, 101 франк к оплате в Париже будет стоить 100 франков в Брюсселе, т.е. курс Парижа в Брюсселе составит 100/101, или 99.01; а 100 франков к оплате в Брюсселе стоят 101 франк в Париже, т.е. курс Брюсселя в Париже составит 101/100, или 101. Парижские дебиторы пошлют 1000 франков в Брюссель, поскольку их кредиторы должны быть оплачены полностью, например, отправкой металлических денег; кроме того, они понесут потери на обменном курсе, а брюссельские дебиторы, в принципе, получат соответствующую курсовую премию.
310. Но, скажут нам, если бы Париж был должен Брюсселю 200000 франков, а Брюссель Парижу — только 100000 франков, то соответствующие курсы Парижа в Брюсселе и Брюсселя в Париже были бы 100/200 и 200/100, иными словами, 200 франков к оплате в Париже стоили бы 100 франков в Брюсселе, а 100 франков к оплате в Брюсселе стоили бы в Париже 200 франков! Конечно, нет: такая абсурдная ситуация была бы невозможной. Имеется предел для курсовых потерь и премий: этот предел — общие издержки на транспортировку, включая риски, 100 франков наличными из одного места в другое. До тех пор пока курсовая потеря не достигает этого предела, дебитор предпочитает купить вексель или выставить вексель на себя вместо того, чтобы посылать деньги. Как только предел достигнут, и тот и другой способ ему безразличен. Если же предел превышен, он предпочтет высылать деньги, так что данный предел не может превышаться.
311. Курно в своих Исследованиях о математических принципах теории богатства посвятил обменным курсам специальную главу. Я позволю себе отослать читателя к этой работе за более полными сведениями и ограничусь лишь тем, что позаимствую у автора его общую формулировку обменного курса.
Обозначим два рынка (1) и (2), обозначим сумму задолженности рынка (1) рынку (2) через m1,2, сумму задолженности рынка (2) рынку (1) через m2,1, курс обмена рынка (1) на рынке (2) — через с1,2, а курс обмена рынка (2) на рынке (1) — через с2,1. В пределах сумм, определяемых объемом издержек на транспортировку денег, имеем
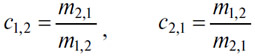
два уравнения, из которых следует также
Итак: Обменные курсы равны обратным отношениям сумм, подлежащих передаче.
Они взаимно обратны.
Это отношение напоминает отношения цен (§ 44), как и должно быть, поскольку курсы есть по определению не что иное, как цены на каждом рынке единицы или определенного количества денег, подлежащих оплате на всех остальных рынках.
312. Формула
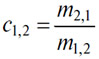
применима в случае, когда две страны имеют одни и те же деньги, например, золотые монеты. Тогда торговец, который должен перевести деньги с рынка (2) на рынок (1) и который имеет необходимое для этой цели золото, покупает вексель, если m2,1/m1,2 < 1+γ, где γ — издержки транспортировки единицы золота из (2) в (1); или же посылает золото, если m2,1/m1,2 стремится стать >1+γ. Таким образом, 1+γ представляет собой постоянный предел обменного курса.
Если у двух стран разные деньги, то формула курса (1) в (2) приобретает следующий вид:
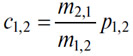
где p1,2 — цена денежной единицы рынка (1) в деньгах рынка (2). Обычно курс c1,2 объявляется без указания значений двух определяющих его величин m2,1/m1,2 и p1,2; однако теоретически и практически во многих случаях имеет смысл различать эти два фактора. Один из них обозначает отношение соответствующих задолженностей и кредитов двух рынков и является курсом в собственном смысле слова, а другой — отношение стоимостей двух денежных единиц, его можно назвать ажио.
Итак, если теперь на рынке (2) обращается денежная единица, конвертируемая в денежную единицу рынка (1), например, серебряные деньги, обмениваемые на золотые, и если у торговца из (2) есть серебро, то он покупает вексель, если (m2,1/m1,2)p1,2 < p1,2+γ, где γ — издержки по доставке денег из (2) в (1); или посылает серебро, если (m2,1/m1,2)p1,2 стремится стать > p1,2 + γ. Таким образом, на этот раз предел обменного курса оказывается переменным. Но если денежная единица рынка (2) не может быть обменена на денежную единицу рынка (1), например, бумажные деньги с принудительным курсом, то торговец имеет бумажные деньги, которые он не может отправить ни в каком случае. Какими бы ни были m2,1/m1,2 и p1,2, ему придется покупать или вексель, или золото. В этом случае нет никакого предела обменному курсу.
313. Пусть (1), (2), (3), (4). — неопределенное количество обменных рынков, c2,1 и c3,1 — курс рынков (2) и (3) на рынке (1), c3,2 — курс рынка (3) на рынке (2). Путем рассуждений, аналогичных проведенным ранее для случая обмена нескольких товаров между собой на одном рынке (112), нетрудно доказать, что общее равновесие между курсами может быть лишь тогда, когда в общем случае будет соблюдаться соотношение
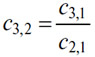
Итак: В состоянии общего равновесия курс двух каких-либо рынков, одного на другом, равен отношению курсов и того, и другого на каком-либо третьем.
314. Если такое состояние общего равновесия не достигнуто, то оно установится посредством арбитражей по отношению к векселям точно так же, как это происходит по каким-либо товарам (114). Векселя — это как раз и по преимуществу тот товар, по которому проводятся арбитражные операции. В каждом торговом месте есть специализированные банкиры, называемые камбистами, ежедневно следящие за курсами и приводящие их к состоянию общего равновесия, извлекая выгоду из замены прямых покупок косвенными или, точнее говоря, из комбинации покупки или продажи косвенным путем с продажей или покупкой прямым путем. Их деятельность приводит к двум очень важным последствиям.
315. Отсюда следует прежде всего, что курсы в одном месте на все остальные не определяются простым отношением кредитов и долгов данного рынка с каждым из остальных, а зависят более сложным образом — от отношения кредитов и долгов данного рынка со всеми остальными. Иначе говоря, курсы одной страны с другими странами колеблются в одно и то же время и в одном и том же направлении в зависимости от того, сводится ли общий итог торговли этой страны с заграницей с избытком экспорта над импортом, или наоборот. Если страна продала больше, чем купила, то курс ее ценных бумаг будет подниматься выше паритета; если она купила больше, чем продала, то ее курс будет опускаться ниже паритета. В старой так называемой системе торгового баланса это называлось иметь курс для себя или против себя, иметь благоприятный и неблагоприятный курс. Эти выражения относились к тому, что импорт драгоценных металлов считался выгодным, а экспорт — невыгодным делом. В этом плане представления существенно изменились, и тем не менее надо знать, что в зависимости от того, имеет ли страна курс для себя или против себя, она ввозит или вывозит деньги; в первом случае это приводит к повышению цен и, следовательно, к росту импорта и снижению экспорта, а во втором — к снижению цен и, следовательно, к сокращению импорта и увеличению экспорта; так что в обоих случаях равновесие само собой стремится к установлению.
316. Второй результат арбитража на вексельных курсах — это практический результат, имеющий неоценимое значение. Он состоит в том, что расчеты по огромной массе международных сделок с товарами и услугами осуществляются при минимальном участии золота или серебра. Не так давно международные обязательства и погашение долгов от страны к стране были связаны почти целиком с импортом и экспортом товаров, т.е. продукции сельского хозяйства, промышленности и торговли. Сегодня большое число разных элементов входит в состав этих долгов и кредитов. Важнейшие из них перечисляет Жорж Гошен в своей Теории курсов иностранной валюты. Эти элементы таковы: импорт и экспорт кредитных обязательств, государственных ценных бумаг, акций промышленных предприятий, оплата и получение долгов по этим ценным бумагам, выплата прибылей, комиссионных вознаграждений и брокерских комиссий, расходы граждан данной страны за границей и т.д. и т.п. К примеру, ежегодный избыток импорта собственно товаров над их экспортом составляет для Англии несколько сотен миллионов, а свой баланс она восстанавливает за счет фрахта осуществляемых ею морских перевозок, комиссионных и брокерских вознаграждений за проводимые ею коммерческие и банковские операции, [за счет] доходов на ее капиталы. Таковы те деловые операции, которые регулирует торговля векселями. Париж должен Брюсселю, но ему должны Амстердам или Франкфурт. Первый из этих избытков оплачивается за счет второго. Таким образом, всемирный рынок векселей играет роль обширной клиринговой палаты, где сделки всего мира осуществляются просто путем оплаты разностей. И этот результат достигается исключительно при помощи предоставленного самому себе механизма свободной конкуренции. Закон предложения и спроса управляет всеми обменами товаров, как закон всемирного тяготения управляет всеми движениями небесных тел. Система экономического мира выступает здесь, наконец, во всей полноте и сложности, и, быть может, представляется столь же прекрасной в своем сочетании необъятности и простоты, как и астрономическая система звездного мира.
