Решение уравнений обращения и денег

Содержание:

• 278. Решение уравнений обращения. Закон установления цены услуги денег и цены денег.
• 279. Закон изменения этих цен.
• 280. Случай товара-денег: существующий продукт, сырой материал. Закон установления и изменения цены в этих разных случаях.
• 281. Случай одного товара, играющего роль денег и счетного товара. Закон установления цены. Уравнение денежного обращения. Норма дохода, норма процента и дисконт.
• 282. Изменения цен, выраженные в счетном товаре — деньгах.
• 283. Геометрическое решение задачи определения стоимости товара-денег. Закон установления этой стоимости.

278. Теперь нам предстоит перейти от теоретического, математического, решения задачи к ее практическому решению, на рынке.

Как было сказано, мы сначала предполагаем, что (U) выступает в качестве денег, не будучи ни товаром, ни счетным товаром (единицей). Эту ситуацию нетрудно представить: так было бы, к примеру, в стране, где обращались бы бумажные франки с принудительным курсом, как это имеет место в настоящее время в Австрии и Италии с их бумажными флоринами и бумажными лирами с принудительным курсом, но где в то же время цены заявлялись бы в металлических франках, золотых или серебряных, как они могли бы, в крайнем случае, заявляться в Австрии и Италии в золотых или серебряных флоринах и лирах. Таким образом p_b... p_m... P_k... p_a', p_b'... p_m'... p_k... p_u' — это цены, выраженные в (A).

Но это обстоятельство позволяет нам считать, что практическое решение задачи в том виде, как оно дано в теориях производства и капитализации, касается и оборотных капиталов. Оборотные капиталы (A'), (B'),... (M)... оказывают свои услуги снабжения точно так же, как основные капиталы (K), (K'), (K'')... оказывают свои потребительные услуги (т.е. услуги в ходе их потребления — Прим. перев.). Цены p'_a, p'_b...p'_m. определяются так же, как и цены p_k, p_k', p_k''..., а цены p_b... p_m... — как цены P_k, P_k', P_k''... И фактически, как мы это уже видели (§§ 275, 276, 277), уравнения капитализации в системах [2], [3], [5], [6], [7] содержат переменные величины или члены, относящиеся к (A'), (B'),... (M)... (U)...; система [1] содержит m+s уравнений предложения, система [4] — m+s уравнений равенства предложения и спроса на (A'), (B'),... (M)..., а система [8] — m+s+1 уравнение равенства нормы чистого дохода на (A'), (B'),... (M)... (U)... Таким образом, вне указанных систем остаются только уравнение [9] предложения и уравнение [10] равенства предложения и спроса на (U). Следовательно, если некоторая цена p'_u объявлена («выкрикнута») наугад и сохраняется в неизменном виде в течение процесса нащупывания производства и капитализации, то мы придем к последнему уравнению, из которого следует равенство цены счетного товара единице и одновременно равенство предложения и спроса по счетному товару, и нам останется только решить уравнение



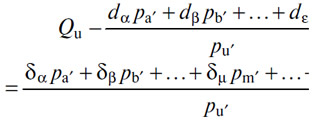
Положим


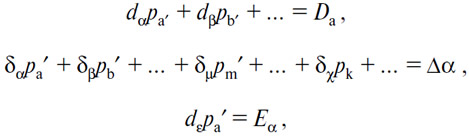
и


это последнее уравнение перепишем как



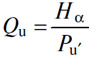
Три члена D_α/p_u, Δ_α/p_u, E_α/p_u, обозначают соответственно оборотные денежные средства в руках потребителей, оборотные денежные средства у производителей и деньги в форме сбережений. Но так как p_u не может отличаться в сбережениях от того, чем она является в обращении, не может отличаться в коммерческом обороте от того, чем она является в текущем обращении, то общая цена услуги денег как средств обращения или как сбережений вытекает из единственного уравнения денежного обращения, указанного выше. Если, следовательно, мы имели бы случайно



то задача была бы полностью решена, но в общем случае мы будем иметь


и нужно прийти к равенству предложения денег и спроса на них путем нащупывания по p'_u.

Обратившись к разным членам, входящим в H_α, легко увидеть, что их нельзя считать независимыми от p_u' так как эта величина фигурирует в члене o_up_u' уравнения обмена. Отсюда, одновременно с уравнениями максимального удовлетворения, получаются величины α, β... ε для некоторого участника обмена, а, следовательно, и d_α, d_β,... d_ε для всех таких участников; однако при всем этом подобная зависимость остается весьма косвенной и слабой. В том смысле, что не хватает малого, чтобы уравнение денежного обращения в случае, когда деньги не являются товаром, оказалось в действительности внешним для системы уравнений экономического равновесия. Если предположить, что это равновесие устанавливается сначала, то интересующее нас уравнение решается затем почти без нащупывания — путем повышения или понижения p_u, смотря по тому, оказалось ли при объявленной наугад цене p'_u количество Q_u<>H_α/p'_u. Но если при этом такое повышение или понижение p_u приводит к очень малому изменению H_α, то остается только продолжить общее нащупывание, чтобы наверняка прийти к равновесию. Именно это и происходит на денежном рынке.


Итак: Цена услуги денег устанавливается путем ее повышения или понижения, в зависимости от того, превышает ли желаемый объем наличности количество денег или не достигает его.

Таким образом, имеется равновесная цена p_u', и если обозначить через i равновесную норму чистого дохода, то единица количества денег будет стоить p_u=p_u'/i. Тогда имеем также p_u'/i=p_u/1; так что, если где-либо наблюдается ажио (расхождение цен денег в разных частях рынка — Прим. перев.), то его величина будет одинаковой как для цены денег, так и для цены его услуги. Иначе говоря, полагая H_α=H_αi, получим


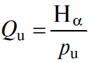
279. После того как мы исследовали установление денежного равновесия, нам надо исследовать его изменения.

С этой целью припишем вещам, не имеющим прямой полезности и, следовательно, редкости в собственном смысле слова — таким, как сырье, производительные услуги, услуга денег, — условные редкости, пропорциональные их ценам. Пусть, таким образом, R_u', R_a', R_b'... R_m',... R_k'... обозначают редкости услуг (U), (A'), (B'), (M). (K). В силу равенства цен отношениям редкостей имеем


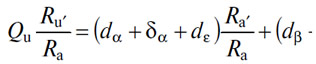
или


то есть, обозначая термином прямоугольная полезность произведение количества на среднюю редкость, видим, что прямоугольная полезность услуги денег есть сумма прямоугольных полезностей товаров и услуг товаров, фигурирующая в желательной денежной наличности. Пусть эта сумма есть H, тогда



и, смотря по тому, приняли ли мы за счетный товар (A), (B)..., получим следующие строгие выражения:


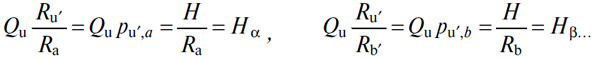
Таким образом, представляется, что при прочих равных условиях в случае, когда деньги не являются товаром, редкость и, как следствие, стоимость услуги денег варьирует прямо пропорционально полезности, когда количество остается тем же, и обратно пропорционально количеству денег, когда полезность остается неизменной. Здесь, однако, есть небольшая трудность. Вполне возможно предположить изменение полезности без изменения количества; однако нельзя предполагать изменение количества без изменения полезности, если только не предположить, что все q_u изменяются при этом в той же пропорции. Если в такой ситуации p_u' изменяется обратно пропорционально количеству денег, то величины q_up_u', (q_u—o_u)p_u' и o_up_u' останутся неизменными и, следовательно, равновесие сохранится при изменении одной p_u'. За исключением этого особого случая, если количество изменяется, то из-за изменения q_u изменяются o_up_u и, как следствие, все α, β,.. ε, а также d_α, d_β,.. d_ε и все элементы полезности. Это очевидно; однако следует заметить, что в этом общем случае: 1) q_up'_u составляют лишь часть дохода участников обмена и их вариация распределяется между всеми расходами: запасы, потребление, сбережение; 2) если вследствие непропорционального изменения величин q_u все q_bp'_b, (q_u—o_u)p'_u и op вырастут или уменьшатся для некоторых участников обмена, то они будут снижаться или расти для других и, таким образом, величины d_α, d_β,.. d_ε, δ_α, δ_β,... δ_μ… δχ… изменятся незначительно; 3) величины d_α, d_β,.. d_ε, δ_α, δ_β,... δ_μ… δχ… и R_u', R_a', R_b'… R_m',… R_k'… изменяются в разных направлениях, откуда следует, что если эти количества изменяются незначительно, то их произведения (или прямоугольные полезности) будут изменяться еще меньше вследствие колебаний количества денег. Таким образом, с очень высокой степенью точности можно утверждать, что: — Редкость или стоимость услуги денег прямо пропорциональна их полезности и обратно пропорциональна их количеству.

В силу соотношения p_u=p_u'/i это утверждение должно относиться как к редкости или стоимости самих денег, так и к редкости или стоимости их услуги. Иначе говоря, полагая H=Hi, H_α=H_αi, H_β=H_βi..., получим


280. В отличие от прежних времен, когда, как говорят, деньгами служил скот, сегодня уже нельзя думать о том, чтобы взять в качестве денег какой-либо капитал — земельный, движимый или личный. Каждый из этих капиталов представлен слишком разными видами, что весьма затрудняет его определение. Все они обладают недостаточной редкостью и ценой, как только они поделены на мелкие части, впрочем, их трудно, если не невозможно, делить и сохранять. Нельзя также взять и услугу, вещь нематериальную. Можно взять только продукт или сырой материал. Сама природа словно озаботилась тем, чтобы сосредоточить свойства, которыми должны обладать деньги: однородность, большую редкость, делимость, неизменность — в двух драгоценных металлах: золоте и серебре, которые одновременно и продукты, и сырые материалы^*. Поэтому нам будет достаточно выяснить, как устанавливается цена такой вещи, которая есть одновременно деньги и продукт или деньги и сырой материал.

Мы знаем, что цена p_b' услуги снабжения существующего продукта (B') следует из уравнения


где Δ_b' — непрерывно убывающая функция от p_b', а O_b' — функция от p_b', последовательно возрастающая от нуля, а затем убывающая до нуля, когда аргумент стремится к бесконечности (§ 276).

Мы знаем также (§ 276), что цена p_m' услуги снабжения существующего сырого материала (M) следует из уравнения


где Δ_m' — непрерывно убывающая функция от p_m', а Q_m — заданное число.

Если ввести член, выражающий спрос на услугу денег, в оба эти уравнения, то они примут вид


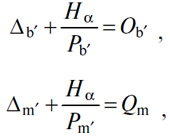
или


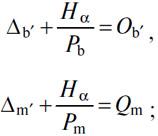
и все они, как до, так и после введения члена, относящегося к деньгам, разрешаются путем повышения или понижения цены смотря по тому, превышает ли спрос предложение или предложение — спрос. Только после введения члена, относящегося к деньгам, равновесная цена, разумеется, выше, чем до этого; кроме того, если предположить, что решение путем нащупывания находится на двух разных рынках, следует допустить, что происходят операции переноса некоторого количества с товарного рынка на денежный или обратно до тех пор, пока цены товара и денег не сравняются.

Итак: Выбор одного товара в качестве денег поднимает его цену това-ра-денег выше его цены в качестве неденежного товара.

Общая и равная цена товара-денег, или его услуги как товара и как денег, устанавливается путем дополнительной чеканки монет или демонетизации (переплавки денег в слитки) в зависимости от того, оказывается ли цена денег выше цены товара, или наоборот.

Что же касается закона изменения цены товара-денег в прямой пропорции к полезности и в обратной пропорции к количеству, то он в высокой степени точен в том, что касается денег, в силу следующего обстоятельства: поскольку количества и редкости товаров изменяются в противоположном направлении, то прямоугольная полезность той доли товара-денег, которая представлена в денежной наличности, остается примерно одной и той же как до, так и после назначения товара в качестве денег; так что H и H всегда остаются примерно постоянными. Но этот закон более или менее верен и в том, что касается товара и, как следствие, товара-денег, в связи с тем, что функции спроса более или менее убывают вместе с ростом цен, а функции предложения остаются более или менее неизменными.

281. Закон прямой пропорциональной зависимости стоимости денег от их полезности и обратной зависимости их стоимости от количества дает нам простой способ перейти от случая, когда деньги не являются ни товаром, ни счетной единицей, к случаю, когда деньги — и товар и счетная единица одновременно.

Данный закон, как мы уже говорили, не является абсолютно строгим. Однако он является таковым, по крайней мере, в том, что касается количества, если: 1) мы стоим, как мы это делали, на статической точке зрения установления равновесия с «нуля», предполагая, что потребители — земельные собственники, работники и капиталисты — обладают основными и оборотными капиталами и одалживают их производителям-предпринимателям; и 2) количество денег в руках капиталистов варьирует пропорционально. Действительно, в этом случае, поскольку члены o_up_u' уравнений обмена не изменяются, в рамках гипотезы об обратной пропорциональности стоимости и количества, то экономическое равновесие сохраняется, в рамках той же гипотезы.

Итак, предположим, что (U) становится (A') и что количество Q_u и цена p_u' (U) становятся количеством Q''_a' и ценой p_a' (A'), так что


Тогда (A'), будучи уже счетным товаром, становится также деньгами. Совокупное количество Q_a' подразделяется на количество Q'_a', оборотный капитал, и Q''_a', деньги. Цена услуги оборотного капитала p_a' по-прежнему определяется из уравнения


(§ 276), которое можно представить в виде


та же цена p_a, услуги денег определяется из уравнения


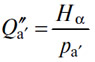
(§ 278), так что


Итак: В случае, когда один товар является деньгами и счетным товаром, общая и одинаковая цена услуги этого товара в качестве оборотного капитала и в качестве денег устанавливается путем ее повышения или понижения в зависимости от того, является ли спрос больше или меньше количества; эта цена удерживается посредством чеканки монет или демонетизации, смотря по тому, оказывается ли цена услуги денег выше или ниже цены услуги оборотного капитала.

После того как цена p_a' таким образом определена, следует провести специальное нащупывание относительно капитализации, которое дает


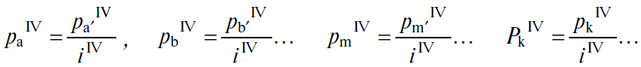
(§§ 256, 257,258). После этого получаем


где D^IV_a + D^IV_a' — совокупное количество (A), которое надлежит произвести (§ 259). И теперь остается только провести последнее нащупывание, которое одновременно приведет к равенству себестоимости (А) единице и равенству действительного предложения (A) и действительного спроса на него. Тогда p_a'=p_ai=i, и окончательно получаем


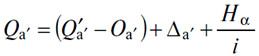
Поскольку роль (A') как оборотного капитала обычно малозначительна по сравнению с ролью в качестве денег, то уравнение


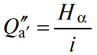
особенно существенно. Оно может быть заменено (§ 278) тремя уравнениями


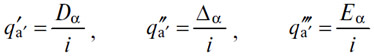
последнее из которых, значительно более важное, чем два первых, в свою очередь может быть заменено двумя следующими:


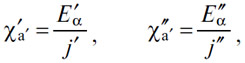
первое из которых задает ставку процента j' на рынке основного капитала, а второе — ставку дисконтирования j'' на рынке оборотного капитала; j' и j'' колеблются вокруг нормы чистого дохода i, но по разным причинам могут более или менее отличаться от нее, временно или же в течение продолжительного периода.

282. Таково, в целом и в деталях, уравнение равенства предложения (A') и спроса на него для того случая, когда (A') является товаром-деньгами и счетным товаром:


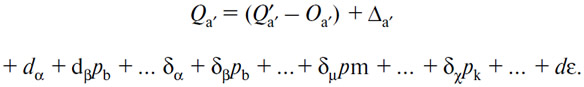
В этом случае товара-денег и счетного товара особенно примечателен способ понижения или повышения всех цен, выраженных в (A), через которое выражается увеличение или уменьшение редкости или стоимости этого товара в качестве денег, вытекающее из уменьшения или увеличения его количества. Предположим, что, после того как равновесие установилось, количество Q_a' и, как следствие, количества и Q'_a' и Q''_a' увеличиваются или уменьшаются, и покажем, каким образом сам факт увеличения или уменьшения Q''_a' на денежном рынке оказывается достаточным для повышения или снижения всех цен, не говоря о прочих сопутствующих фактах. В соответствии с уравнением


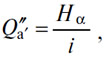
на денежном рынке осуществляют снижение или повышение ставки процента i, вслед за которым потребители увеличивают или уменьшают желаемый запас наличности, представляющий количества (A'), (B')... d_α, d_β..., являющиеся убывающими функциями от p_a'=i, p_b'=p_bi... и, следовательно, от i. Но, поскольку количество продуктов не увеличилось, эти намерения приводят только к повышению или снижению цен p_b... Видя такое повышение или снижение цен продуктов, предприниматели предполагают развивать или же ограничивать свое производство, тем более что для них снижение или повышение ставки процента — одна из причин увеличения прибылей или потерь; но они доходят лишь до повышения или снижения цен производительных услуг, количество которых не изменилось. Это повышение или снижение побуждает капиталистов, располагающих более или менее значительными сбережениями, предъявить больший или меньший спрос на новые капиталы; но, так как количество этих капиталов остается все время тем же, их цены просто повысятся или упадут. А когда повышение или снижение распространяется, таким образом, на всю систему, то ставка процента становится той, что была.

283. При принятии нашей последней гипотезы о товаре-деньгах то обстоятельство, что этот товар-деньги является одновременно счетным, затрудняет исследование эффектов совмещения роли товара и роли денег в их воздействии на цены в силу того, что, поскольку цена счетного товара всегда равна единице, то есть равна 1, данные эффекты выражаются не в колебаниях в сторону повышения или снижения цены товара-деньги, а в колебаниях вниз или вверх цен всех товаров. Есть очень простой способ обойти эту трудность: предположить, что товар-деньги не является более счетным, и исследовать последствия совмещения его двух ролей в воздействии на его цену, выраженную в каком-либо другом товаре, например (B).

Итак, предположим, что в качестве денег берется сырой материал (A), имеющийся в целом в количестве Q_a, часть Q'_a которого останется в форме товара, тогда как часть Q''_a примет форму денег, и чья цена, следовательно, выраженная в (B), поднимется с p_a до P_a, а эта последняя цена должна будет удовлетворять уравнению


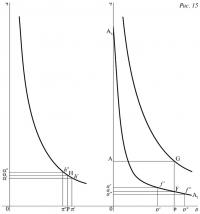
Пусть нам дана теперь (рис.15) прямоугольная система координат, где ось абсцисс — это ось цен O_p, а ось ординат — ось количеств O_q.

Кривая цены денег (A), выраженная в другом товаре (B) в зависимости от количества, аппроксимируется равнобочной гиперболой h''Hh', асимптотически стремящейся к осям координат, чье уравнение


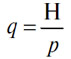
задает такую кривую, что произведение ее ординат, представляющих количества денег (A), на абсциссы, представляющие цены денег (A), выраженные в (B), постоянно и равно значению желаемого объема наличности H, выраженному в (B) и предполагаемому определенным.

Но, с другой стороны, мы знаем (§ 280), что кривая цены сырого материала (A), выраженная в (B), как функция от количества, аппроксимируется кривой A_qA_p, уравнение которой


определяет такую кривую, что количество (A) постоянно убывает начиная с некоторой величины, обозначенной на рисунке отрезком OA_q, до нуля, тогда как цена (A) постоянно возрастает с нуля до некоторой цены, конечной или бесконечной, обозначенной отрезком OA_p.

После этого нетрудно понять, что кривая цены (А), рассматриваемого одновременно как товар и как деньги, выраженная в (B), как функция от количества, есть кривая, проходящая через точку G, чье уравнение


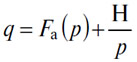
Графически эту кривую можно построить, нанеся для каждого значения абсциссы суммарные значения соответствующих ординат кривой h''Hh' и кривой A_qA_p. Осуществив такое построение, обозначим общее количество товара (A), Q_a, через отрезок OA на графике. Если теперь провести горизонтальную линию AG до пересечения с верхней кривой в точке G и опустить из этой точки перпендикуляр GP, то мы получим абсциссу OP, представляющую цену P_a товара и денег (A), соответствующую имеющемуся количеству Q_a. Далее, отрезки Oa=PF и aA=Oα=FG представляют соответствующие количества Q'_a товара (A) и Q''_a денег (A) без всякого преобразования товара в деньги, и наоборот.

Если вместо того чтобы разделить количество Q_a на Q'_a и Q''_a, как мы это сделали выше, мы бы разделили его случайным образом на два количества, представленных одно через Oa'>Oa, а другое — через a'A=Oα'<Oa, то цена товара (A) была бы представлена Op'<OP, а цена денег (A) — отрезком Oπ'>OP, и тогда надо было бы преобразовать товар в деньги, что уменьшило бы Oa', увеличило Oα' и, следовательно, увеличило бы Op' и уменьшило Oπ'. А если бы мы разделили случайным образом количество Q_a на два количества, представленных одно через Oa''<Oa, а другое — через a''A=Oα''>Oa, то цена товара (A) была бы представлена величиной Op''>OP, а цена денег (A) — величиной Oπ''<OP, и надо было бы преобразовать деньги в товар, что увеличило бы Oa'', уменьшило Oα'' и, следовательно, уменьшило бы Op'' и увеличило Oπ''. Таким образом, наше построение вполне дает геометрическое решение задачи определения: 1) цены товара-денег (A); 2) количества товара (A); и 3) количества денег (A) так, как это и происходит в реальности.

Две кривые, h''Hh' и A_qA_p и расстояние OA, будучи, таким образом, элементами установления цены товара-денег и определения соответствующих количеств товара и денег, являются тем самым и элементами изменения этой цены и этих количеств. Поэтому, чтобы представить геометрически все явления изменения цены товара-денег и соответствующих количеств товара и денег, достаточно рассмотреть последовательно эффекты сдвига кривых h''Hh' и A_qA_p и эффекты изменений расстояния OA. Например, кривая h''Hh' удаляется или приближается к началу координат в зависимости от увеличения или уменьшения величины желаемых запасов наличности; кривая A_qA_p удаляется или приближается к началу координат в зависимости от увеличения или уменьшения полезности (A) как товара. А в зависимости от того, удаляются ли обе эти кривые от начала координат или приближаются к нему, цена (А) увеличивается или уменьшается. Что же касается расстояния OA, то оно увеличивается или уменьшается с увеличением или уменьшением количества (A). А в зависимости от того, увеличивается это расстояние или уменьшается, цена (A) снижается или растет.

Примечания

* См. Etudes d’économie politique appliquée. Théorie de la monnaie, 11.

*** Для упрощения набора я сохраняю здесь обозначение H, которое я использовал в двух предыдущих изданиях, вместо того чтобы ввести здесь обозначение HP, использованное выше (§ 279) для обозначения желаемого объема кассовой наличности, выраженного в счетном товаре (B). Следует также отметить, что мы сочетаем здесь цену (A) денег с ценой (А) сырого материала, а не цену услуги (А) денег с ценой услуги (А) сырого материала.