Формула математического решения задачи обмена нескольких товаров

Содержание:

• 117. Общий случай с держателями нескольких товаров.
• 118. Уравнение эквивалентности обмениваемых количеств. Уравнения максимального удовлетворения. Уравнения частичного спроса или предложения.
• 119, 120, 121, 122. Условие предложения, равного имеющемуся количеству. Следствия.
• 123. Система из m—1 уравнений равенства совокупных спроса и предложения.
• 124. Об обмене нескольких товаров друг на друга на рынке.
• 125. «Выкрикиваемые» (объявляемые) цены: цены в счетном товаре, предполагающие общее равновесие. Определение без расчета частичных объемов спроса или предложения в соответствии с условием максимального удовлетворения.
• 126, 127. Неравенство совокупного спроса и совокупного предложения.
• 128. Изменения совокупных спроса и предложения в связи с изменением цен от нуля до бесконечности.
• 129, 130. Следует увеличить цены, когда спрос больше предложения, и уменьшить их, когда предложение больше спроса.

117. В случае обмена некоторого числа товаров, как и в случае обмена двух товаров друг на друга, уравнения частичного действительного спроса математически определены условием максимального удовлетворения потребностей. Каково же это условие? Оно всегда состоит в том, чтобы отношение редкостей двух некоторых товаров было равно цене одного из них в другом; если этого нет, то между ними выгодно провести обмен. Если обменивающиеся лица являются держателями лишь одного товара и если, оставляя место арбитражным операциям, выкрикивают m(m—1) цен m товаров попарно, цен, не удовлетворяющих условию общего равновесия, то максимальное удовлетворение будет иметь место для каждого обменивающегося лица тогда, когда отношения редкостей запрашиваемых товаров к редкости имеющегося у него товара будут равными, но не объявляемым («выкрикиваемым») ценам, а настоящим ценам, получаемым путем арбитражных операций. Но если обменивающиеся лица являются держателями нескольких товаров и если — чтобы, напротив, избежать арбитражных операций — объявляются m—1 цен m—1 товаров в m-м товаре, принимаемом за счетный, имея в виду, что цена двух товаров одного в другом будет равна отношению цен одного и другого в счетном товаре, то очевидно, что максимальное удовлетворение будет иметь место для каждого обменивающегося лица тогда, когда отношения редкостей товаров, исключая счетный, к редкости этого счетного товара будут равны объявляемым ценам.


118. Итак, пусть дано обменивающееся лицо (1), держатель q_a,1 товара (А), q_b,1 (В), q_c,1 (С), q_d,1 (D). Пусть r=φ_a,1(q), r=φ_b,1(q), r=φ_c,1(q), r=φ_d,1(q)- — уравнения полезности или потребности в товарах (А), (В), (С), (D). для этого обменивающегося лица в течение некоторого времени. Пусть p_b, p_c, p_d... — соответствующие цены товаров (В), (С), (D)... в товаре (А). И пусть x₁, y₁, z₁, w₁... — соответствующие количества (А), (В), (С), (D)..., которые обменивающееся лицо (1) добавит к количествам q_a,1, q_b,1, q_c,1, q_d,1..., держателем которых он является по ценам p_b, p_c, p_d.... Эти количества могут быть положительными, и тогда они представляют собой запрашиваемые количества; они могут быть отрицательными и представлять собой количества предлагаемые. И, так как наше обменивающееся лицо сможет предъявлять спрос на некоторые товары лишь при условии, что он предлагает в эквивалентном количестве некоторые другие товары, очевидно, что среди данных количеств x₁, y₁, z₁, w₁... одни положительны, а другие отрицательны и что все они будут связаны уравнением


К тому же, поскольку мы предположили состояние максимального удовлетворения, те же самые количества связаны системой уравнений


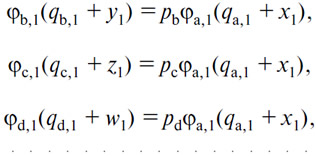
т.е. m—1 уравнений, образующих вместе с предыдущими m уравнений, в числе которых можно предположить, что последовательно устраняются m—1 неизвестных x₁, y₁, z₁, w₁. так, что остается лишь одно уравнение, дающее m-ое в виде функции от цен. Таким образом, мы получаем следующие уравнения спроса или предложения (В), (С), (D)... со стороны обменивающегося лица (1):



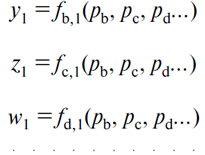
при этом спрос или предложение (А) тем же самым лицом дается уравнением


Таким же образом мы получим следующие уравнения спроса или предложения (В), (С), (D)... со стороны обменивающихся лиц (2), (3)...


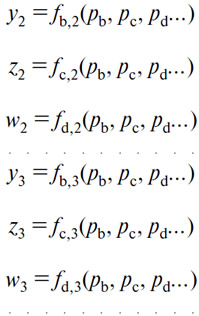
и так далее, при этом спрос или предложение (А) со стороны тех же самых лиц дается уравнениями


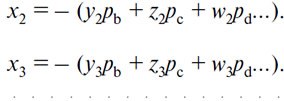
Именно таким образом намерения к торгу всех обменивающихся лиц могут быть выведены из полезности разных товаров для каждого из них и из количества этих товаров, которым каждый из них обладает. Однако, прежде чем идти дальше, надо сделать здесь весьма важное замечание.


119. Может быть так, что при некоторых ценах p_b, p_c, p_d...y₁ является отрицательным: это тот случай, когда обменивающееся лицо (1) предлагает товар (В) вместо того, чтобы спрашивать его. Может быть даже так, что y₁ равняется —q_b,1: это случай, когда данное лицо не оставляет у себя товара (В). Если ввести это значение y₁ в систему из m—1 уравнений максимального удовлетворения, то они примут вид


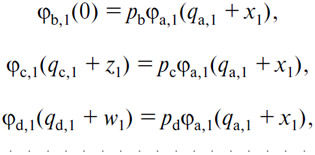
И, устраняя p_b, p_c, p_d. из этих уравнений и из уравнения


получаем уравнение


Данное уравнение является уравнением условия, которое может быть выражено в следующих терминах: чтобы предложение одного из товаров могло быть равно имеющемуся количеству этого товара, необходимо, чтобы можно было вписать в часть плоскости кривых потребности в запрашиваемых товарах, лежащую выше части, представляющей потребности, удовлетворенные имеющимся количеством, такие прямоугольники, суммарная площадь которых была бы равна площади прямоугольника, имеющего в качестве высоты наличное количество предлагаемого товара и в качестве основания — интенсивность максимальной потребности в этом товаре.


Данное условие либо выполняется, либо нет. Если оно выполняется, то предложение (В) со стороны лица (1) может равняться в некоторых случаях количеству q_b,1, держателем которого он является. Впрочем, оно никогда не может быть больше этого количества. Важно, следовательно, отметить, что для всех значений p_b, p_c, p_d..., при которых отрицательный y₁ становится больше q_b,1 в уравнениях спроса и предложения (В), данное уравнение должно быть заменено на уравнение y₁=—q_b,1.

120. Но это не все. Прежде всего такое же замечание приложимо к уравнениям спроса или предложения (С), (D). при значениях p_b, p_c, p_d..., при которых отрицательные z₁, w₁... становятся больше q_c,1, q_d,1... Затем, как раз в том случае, когда эти уравнения должны быть заменены на уравнения z₁=—q_c,1 , w₁=—q_d,1..., уравнение спроса или предложения (В) должно быть изменено соответствующим образом.

Так, при z₁=—q_c,1, например, система уравнений, дающая спрос или предложение (В) лица (1), примет следующий вид:


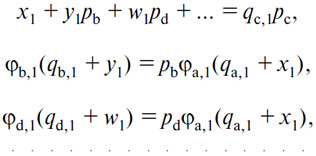
т.е. m—1 уравнений, из которых можно предположить, что последовательно устраняются m—2 неизвестных, такие, как x₁, w₁,... так, что остается лишь одно уравнение, дающее y1 в виде функции от p_b, p_c, p_d. Так же и при w₁=—q_d,1... Так же, наконец, — что понятно и без дальнейших разъяснений — в том случае, когда предложение не только одного из товаров (С), (D)..., но и двух, трех, четырех... и, в общем виде, некоторого числа из них, равно имеющемуся количеству.

121. Мы ничего не сказали об уравнении спроса или предложения счетного товара (А), имеющем особую форму. Прежде всего очевидно, что при значениях p_b, p_c, p_d..., при которых отрицательный х₁ становится больше по абсолютной величине q_a,1, и это уравнение тоже должно быть заменено на уравнение x₁=—q_a,1, кроме того, в этом случае система уравнений, определяющая спрос или предложение (А) со стороны лица (1), примет следующий вид:


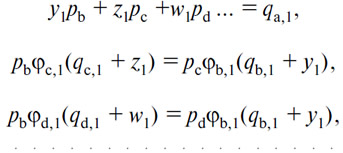
т.е. всё также m—1 уравнений, из которых можно было бы последовательно устранить m—2 неизвестных такие, как z₁, w₁... так, что остается лишь одно уравнение, дающее у₁ как функцию от p_b, p_c, p_d...

122. Разумеется, было бы более или менее сложно расположить уравнения спроса или предложения таким образом, чтобы они удовлетворяли данным ограничениям; тем не менее столь же очевидно, — и это главный пункт, — что, как только объявлены определенные цены p'_b, p'_c, p'_d (В), (С), (D) в (А), то, учитывая факт равенства предложения имеющемуся (наличному) количеству, запрашиваемые и предлагаемые количества всех товаров в полной мере определены. Покажем это.

Пусть q=ψ_a,1(r), q=ψ_b,1(r), q=ψ_c,1(r), q=ψ_d,1(r)... есть уравнения полезности (А), (В), (С), (D). для обменивающегося лица (1), которые, предположим, решены относительно количеств, но уже не относительно редкостей. Тогда после обмена получим:


и, кроме того, согласно условиям эквивалентности обмененных количеств и максимального удовлетворения, имеем:


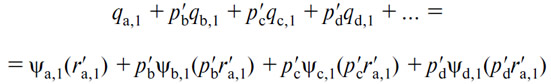
Последнее уравнение дает r'_a,1. С помощью r'_a,1 имеем r'_b,1, r'_c,1, r'_d,1. и, следовательно, х'₁, y'₁, z'₁ , w'₁, а единственными товарами, которые следует удержать для себя или приобрести, являются те, для которых интенсивность первой потребности, подлежащей удовлетворению, больше, чем произведение цены и r'_a,1.

Если r'_a,1 больше интенсивности первой потребности в (А), то лицо (1) не предъявляет спроса на счетный товар или не оставляет его у себя.

123. Допустив, что уравнения спроса или предложения (А), (В), (С), (D)... со стороны обменивающихся лиц (1), (2), (3)... расположены должным образом, дабы удовлетворить предыдущим ограничениям, обозначим через X, Y, Z, W ... суммы х₁+х₂+х₃ + ... y₁+y₂+у₃ + ... z₁+z₂+z₃+ ... w₁+w₂+w₃+ ... и через F_b, F_c, F_d... суммы функций ƒ_b,1, ƒ_b,2, ƒ_b,3....ƒ_c,1, ƒ_c,2, ƒ_c,3....ƒ_d,1, ƒ_d,2, ƒ_d,3.... Так как условие равенства предложения и спроса на товары (А), (В), (С), (D)... выражается — в общем случае, который нас интересует — уравнениями X=0, Y=0, Z=0, W=0 ..., то для определения текущих равновесных цен мы имеем уравнения


или m—1 уравнений. Впрочем, очевидно, что, так как p_b, p_c, p_d... являются по сути положительными, и если данные уравнения удовлетворяются, т.е. если мы имеем Y=0, Z=0, W=0..., то мы получим также


124. Таким образом определяются математически m—1 цен m—1 из m товаров в m-ом товаре, взятом в качестве счетного в силу тройного условия: 1) что каждое обменивающееся лицо получает максимальное удовлетворение своих потребностей, так как отношения редкостей равны ценам; 2) что каждый должен получить пропорционально тому, что отдает, и отдать пропорционально тому, что получает, так как для каждого товара есть лишь одна цена в счетном товаре — цена, при которой совокупный действительный спрос равен совокупному действительному предложению; 3) что нет места арбитражным операциям, так как равновесная цена двух товаров, одного в другом, равна отношению равновесных цен того и другого в некотором третьем товаре. Посмотрим теперь, каким образом та же самая задача обмена нескольких товаров между собой, чье научное решение мы только что выяснили, является также задачей, которая на рынке решается эмпирически через механизм конкуренции.

125. Прежде всего на рынке, благодаря введению счетного товара, как раз происходит сокращение m(m—1) цен m товаров, друг в друге, до m—1 цен m—1 товара в m-ном товаре. Этот последний — счетный товар; что же касается (m—1)(m—1) цен остальных товаров, выражаемых друг в друге, то они подразумеваются равными отношениям цен товаров в счетном товаре в соответствии с условием общего равновесия. Пусть p'_b, p'_c, p'_d... есть m—1 цен (В), (С), (D). в (А), объявляемых наугад. По этим объявленным таким образом ценам каждое обменивающееся лицо определяет свой спрос и свое предложение по (А), (В), (С), (D). Это делается по размышлении, без расчета, но в точности так, как это происходило бы по расчету в соответствии с системой уравнений эквивалентности запрашиваемых и предлагаемых количеств и максимального удовлетворения, дополненной оговоренными ограничениями. Пусть даны x'₁, x’₂, x’₃ ... y'₁, y’₂, y’₃ ... z'₁, z’₂, z’₃ ... положительные либо отрицательные, при этом частичные спрос или предложение соответствуют ценам p'_b, p'_c, p'_d... Если бы совокупные спрос и предложение по каждому товару были равны, т.е. если бы мы сразу же получили Y'=0, Z'=0, W'=0... и, как следствие, X'=0, то обмен произошел бы по этим ценам и задача была бы решена. Но, как правило, совокупные спрос и предложение по каждому товару будут неравными, т.е. мы получим Y'<>0, Z'<>0, W'<>0... и, следовательно, X'<>0. Что же делают в таком случае на рынке? Если спрос больше предложения, то производят повышение цены товара в счетном товаре; если же предложение больше спроса, то производят понижение. Что же нужно доказать, чтобы установить, что теоретическое решение и решение рынка тождественны? Просто то, что повышение и понижение есть способ решения путем нащупывания системы уравнений равенства предложения и спроса.

126. Напомним, что мы имеем уравнение


которое, если обозначить через D'_a, D'_b, D'_c, D'_d... сумму положительных x, y, z, w... и через О'_a, О'_b, О'_с, О'_d сумму отрицательных x, y, z, w..., взятых с положительным знаком, что соответствует ценам p'_b, p'_c, p'_d..., может быть выражено в форме


и заметим, что (поскольку p'_b, p'_c, p'_d... по сути положительны) если среди количеств X=D'_a—O'_a, Y=D'_b—O'_b, Z=D'_e—O'_e, W=D'_d—O'_d некоторые положительны, то остальные отрицательны, и наоборот; т.е. если при ценах p'_b, p'_c, p'_d... совокупный спрос на некоторые товары больше предложения, то предложение остальных товаров больше спроса, и наоборот.

127. Возьмем теперь неравенство


и поставим его в форме


где функция Δ_b представляет сумму положительных у, т.е. D_b, а функция W_b — сумму отрицательных у, взятых с положительным знаком, т.е. O_b. Абстрагируемся от p_c, p_d... и попытаемся найти — предполагая, что эти цены определены и остается определить только p_b — как следует изменять p_b от 0 до бесконечности, чтобы спрос на товар (В) был равен предложению. Нам не известна ни функция F_b, ни функции Δ_b и Ω_b; но из самой природы факта обмена, в том виде, как мы его исследовали, мы можем высказать относительно этих функций соображения, достаточные для того, чтобы показать, как в ходе интересующей нас операции p_b должно принять значение (если оно существует), при котором первая функция проходит через ноль, а две последние приходят к равенству.

128. Что касается сначала функции Δ_b, функции спроса на (В), заданной через цены товаров (А), (С), (D)..., то при p_b=0 она положительна, т.е. при нулевых ценах (В) в (А), (С), (D)... Действительно, при этой цене совокупный действительный спрос на (В) равен превышению полной экстенсивной полезности над совокупным имеющимся количеством, превышению положительному, если товар (В) редкий и является частью общественного богатства. Если p_b растет и вместе с ним пропорционально все цены (В) в (А), (С), (D)..., то функция убывает, поскольку она является суммой убывающих функций. Тогда действительно товар (В) становится все более дорогим по отношению к товарам (А), (С), (D).; но в рамках принятой гипотезы, впрочем, при прочих равных условиях, невозможно допустить, что спрос на него растет; он может лишь уменьшаться. Впрочем, всегда можно предположить достаточно большое значение p_b, даже бесконечное, т.е. достаточно высокие цены (В) в (А), (С), (D)..., чтобы спрос был нулевым.

Что касается затем функции Ω_b, функции предложения (В) в обмен на (А), (С), (D)..., то она равна нулю при p_b=0 и даже при некоторых положительных значениях pb, т.е. при нулевых и даже положительных ценах (В) в (А), (С), (D). Действительно, точно так, как всегда можно допустить цены (В) в (А), (С), (D). достаточно высокими, чтобы спрос на него был нулевым, можно также допустить цены (А), (С), (D)... в (В) достаточно высокими, чтобы спрос на них был нулевым, случай, при котором предложение (В) равно нулю.

Если p_b растет и вместе с ним пропорционально все цены (В) в (А), (С), (D)..., то функция последовательно является возрастающей и убывающей, поскольку она суть сумма последовательно возрастающих и убывающих функций. Тогда действительно товары (А), (С), (D). становятся все менее дорогими относительно товара (В), и спрос на них проявляет себя последовательно в то же самое время, что и сопровождающее его предложение (В). Но данное предложение не возрастает до бесконечности; оно проходит, по меньшей мере, через один максимум, который не может быть больше совокупного имеющегося количества; затем оно убывает и снова становится нулевым, если p_b становится бесконечно большим, т.е. если (А), (С), (D)... бесплатны.

129. В этих условиях, — если только D_b не стало равным нулю до того, как перестало быть равным нулю O_b, случай, при котором нет решения, но такого случая не бывает, когда среди обменивающихся лиц есть держатели нескольких товаров, — существует некоторое значение p_b, при котором O_b и D_b равны. Чтобы найти это значение, надо увеличивать p'_b, если при цене p'_b имеем Y'>0, или D'_b>O'_b, и уменьшать p_b, если при цене p'_b имеем Y'<0, или O'_b>D'_b. Таким путем получаем уравнение


После того как эта операция проведена, неравенство


превращается в


но можно получить уравнение


увеличивая или уменьшая p'_c в зависимости от того, имеем ли мы при цене p'_c Z'>0, т.е. D'_c>O'_c, или же Z'<0, или O'_c>D'_c.

Таким же образом получаем уравнение


и так далее.

130. После того как выполнены все эти операции, имеем


и следует установить, что данное неравенство ближе к равенству, нежели исходное неравенство


Итак, представляется вероятным, если учесть, что замена p'_b на p"_b, приведшая последнее неравенство к равенству, имела как прямое следствие — в том, что касается, по крайней мере, спроса на (В), — изменение в одном направлении, в то время как замена p'_c на p"_c, p'_d на p"_d , удалявшие предыдущее неравенство от равенства, имела косвенные следствия, которые — по крайней мере в том, что касается спроса на (В) — означали изменение в обратном направлении и до определенной степени эти изменения компенсировали друг друга. По этой причине система новых цен p"_b, p"_c, p"_d...ближе к равновесию, чем система старых цен p'_b, p'_c, p'_d , и достаточно продолжать следовать тому же методу, чтобы все больше и больше приближать ее к равновесию.

Таким образом, мы пришли к тому, чтобы сформулировать закон установления равновесных цен в случае обмена нескольких товаров между собой с участием счетного товара следующим образом: если даны несколько товаров, чей обмен происходит с участием счетного товара, то, чтобы по данным товарам достигалосьь равновесие на рынке, или устанавливалась стационарная цена всех этих товаров в счетном товаре, необходимо и достаточно, чтобы при этих ценах действительный спрос по каждому товару был равен его действительному предложению. Если этого равенства нет, то необходимо — для достижения равновесных цен — повышать цену товаров, действительный спрос на которые больше их действительного предложения, и понижать цену товаров, чье действительное предложение больше действительного спроса.