Проблема обмена нескольких товаров между собой

Закон установления цен товаров

Содержание:

• 104. Обобщение обозначений, относящихся к случаю обмена двух товаров друг на друга.
• 105. Об обмене трех товаров друг на друга.
• 106. Уравнения частичного и полного спроса.
• 107. Уравнения обмена.
• 108. Об обмене m товаров друг на друга. Уравнения спроса.
• 109. Уравнения обмена.
• 110. Проблема обмена нескольких товаров поставлена, таким образом, алгебраически, а не геометрически.
• 111. Условие общего равновесия.
• 112, 113, 114. Гипотеза о p_c,b=ap_c,a/p_b,a и a>1. Арбитраж между (В, А, С), (А, С, В), (С, В, А). Понижение p_c,b. Понижение p_b,a. Повышение p_c,a.
• 115. a < 1. Обратные операции и результаты. Уравнения общего равновесия.
• 116. Замена уравнений равенства спроса и предложения по каждому товару на каждый из остальных товаров по отдельности на уравнения равенства спроса и предложения по каждому товару в обмен на все остальные вместе.

104. Теперь речь идет о том, чтобы перейти от исследования обмена двух товаров (А) и (В) к исследованию обмена нескольких товаров (А), (B), (С), (D)... между собой. Для этого нам достаточно должным образом обобщить наши формулы, начиная с того случая, когда обменивающиеся лица являются держателями лишь одного товара.

Теперь обозначим через D_a,b действительный спрос на (А) в (В), Db действительный спрос на (В) в (А), p_b цену (А) в (В), p_b,a, цену (В) в (А). Четыре неизвестные D_a,b, D_b,a, p_a,b, p_b,a связаны двумя уравнениями действительного спроса:


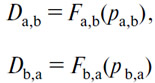
и двумя уравнениями равенства действительных спроса и предложения:


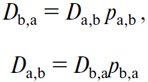
Нам известно, что геометрически два первых уравнения могут быть представлены двумя кривыми, а два последних — двумя прямоугольниками, вписанными в эти кривые так, что их основания равны отношениям их площадей или обратным отношениям их высот.


105. Теперь перейдем сначала от случая с двумя товарами (А) и (В) к случаю с тремя товарами (А), (В) и (С). Для этого представим себе рынок, на который приходят, с одной стороны, люди, имеющие товар (А) и расположенные отдать одну его часть для получения товара (В) и одну часть — для получения товара (С); с другой стороны, люди, имеющие товар (В) и расположенные отдать одну его часть для получения товара (А) и одну часть — для получения товара (С); наконец, люди, имеющие товар (С) и расположенные отдать одну его часть для получения товара (А) и одну часть — для получения товара (В).

Если это так, то взяв из них, например, держателя (В) и проведя должным образом наши предыдущие рассуждения, мы можем сказать — и здесь также, — что намерения данного индивида к торгу поддаются строгому определению.

Действительно, всякий держатель количества q_b товара (В), идущий на рынок для обмена там некоторого количества o_b этого товара на некоторое количество d_a,b товара (А) в соответствии с уравнением обмена:


и некоторого количества o_b,c того же самого товара на некоторое количество d_c,b товара (С) в соответствии с уравнением обмена


придет с рынка с количеством d_a,b (А), количеством d_c,b (С) и количеством y=q_b—o_b,a—o_b,c=q_b—d_a,bv_a/v_b—d_c,bv_c/v_b (В). В любом случае между количествами q_b, v_a/v_b или d_a,b, v_c/v_b или p_c,b, d_c,b и y всегда будет иметь место соотношение:



До прихода на рынок наш человек не знает, какими будут v_a/v_b или p_a,b и v_c/v_b или p_c,b, но он уверен, что узнает это сразу же по прибытии туда и что, зная эти значения p_a,b и p_c,b, он соответственно примет для себя значение d_a,b и значение d_c,b, из которых получится, в конечном счете, значение у в соответствии с приведенным выше уравнением. Разумеется, мы вынуждены признать, что нельзя определить d_a,b, не зная как p_c,b, так и p_a,b, нельзя определить и d_c,b, не зная как p_a,b, так и p_c,b. Но мы вынуждены также согласиться с тем, что, если известны p_a,b и p_c,b, то тем самым поддаются определению и d_a,b и d_c,b.

106. Итак, здесь тоже нет ничего легче, чем выразить математически прямое отношение d_a,b и d_c,b, или действительного спроса на (А) и (С) в (В), к p_a,b и p_c,b, или к цене этих товаров. Данное отношение, соответствующее намерениям к торгу нашего индивида, будет строго выражено двумя уравнениями d_a,b=ƒ_a,b(p_a,bp_c,b) и d_c,b =ƒ_c,b(p_a,b,p_c,b). Таким же образом мы получим уравнения, выражающие намерения к торгу по поводу (А) и (С) всех остальных держателей (В); и, наконец, суммируя просто-напросто эти уравнения частичного спроса, мы получим два уравнения совокупного спроса:


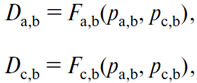
выражающие намерения к торгу всех держателей (В).


Равным образом мы получим два уравнения совокупного спроса:


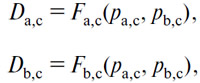
выражающие намерения к торгу всех держателей (С).

Наконец, точно так же мы получим два уравнения совокупного спроса:


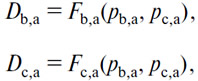
выражающие намерения к торгу всех держателей (А).

107. Впрочем, мы имеем два уравнения обмена:


(B) на (А) и (С).

Мы имеем два уравнения обмена:


(C) на (А) и (В).

Наконец, мы имеем два уравнения обмена:



(А) на (В) и (С).

Итак, имеем, в конечном счете, 12 уравнений с 12 неизвестными, представляющими собой шесть цен трех товаров одного в другом, и шесть совокупных количеств трех товаров, обмениваемых друг на друга.

108. Теперь пусть дано m товаров (А), (В), (С), (D)..., имеющихся на рынке; понятно, что в силу точно таких же рассуждений, как в случае с двумя товарами и в случае с тремя товарами, рассуждений, которые не стоит повторять еще раз, мы можем сформулировать сначала m—1 уравнений действительного спроса на (В), (С), (D)... в (А):


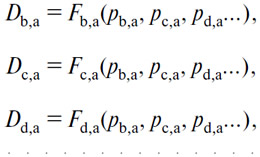
m—1 уравнений действительного спроса на (А), (С), (D)... в (В):


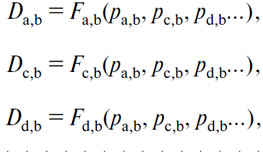
m—1 уравнений действительного спроса на (А), (В), (D)... в (С):


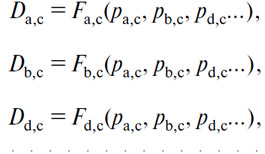
m—1 уравнений действительного спроса на (А), (В), (С)... в (D):


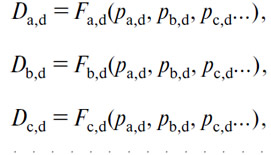
и так далее; таким образом, всего m(m—1) уравнений.

109. С другой стороны, мы можем, разумеется, также сформулировать — без новых объяснений — m—1 уравнений обмена (А) на (В), (С), (D)...


m—1 уравнений обмена (В) на (А), (С), (D)...


m—1 уравнений обмена (С) на (А), (В), (D)...


m—1 уравнений обмена (D) на (А), (В), (С)...


и так далее; итак, снова в общей сложности m(m—1) уравнений.

Эти m(m—1) уравнений обмена вместе с m(m—1) уравнений действительного спроса дают в совокупности 2m(m—1) уравнений. Однако у нас в точности 2 m(m—1) неизвестных; действительно, для m товаров, обмениваемых попарно, имеется m(m—1) цен и m(m—1) совокупных количеств товаров, прошедших через обмен.

110. В особом случае обмена двух товаров друг на друга и в особом случае обмена трех товаров между собой задачу можно решить либо геометрически, либо алгебраически, так как в обоих случаях функции спроса сами можно представить геометрически. В первом случае эти функции являются функциями одной переменной, которые могут быть представлены двумя кривыми. Во втором случае они являются функциями двух переменных, представляемыми шестью поверхностями. Геометрическое решение задачи, следовательно, дает: в первом случае — просто вписание в кривые прямоугольников; во втором — вписание прямоугольников в кривые, получаемые при пересечении поверхностей с плоскостями.

В общем случае, напротив, функции спроса — это функции с m(m—1) переменными, которые не могут быть представлены в пространстве. Вот почему в этом случае сама задача, как представляется, может быть поставлена и решена алгебраически, но не геометрически. Впрочем, давайте вспомним, что речь идет здесь, как и везде, не о том, чтобы поставить и в действительности решить данную задачу в каком-либо из данных случаев, а о том, чтобы научно представить природу задачи, которая встает и эмпирически решается на рынке. Но при такой точке зрения не только алгебраическое решение стоит решения геометрического, но и можно даже сказать, что, выбирая форму анализа (математического), мы выбираем общую и научную форму par excellence.

111. Задача обмена нескольких товаров между собой представляется решенной. Но в действительности она решена лишь наполовину. При определенных выше условиях на рынке будет иметь место некоторое равновесие цен товаров, взятых попарно; но это будет лишь несовершенное равновесие. Совершенное или общее равновесие рынка имеет место лишь в том случае, если цена двух каких-либо товаров, одного в другом, равна отношению цен и того, и другого в каком-либо третьем (товаре). Именно это и следует доказать. Для этого из всех имеющихся товаров возьмем три, например, (А), (В) и (С); предположим, что цена p_c,b больше или меньше, чем отношение цен p_c,a и p_b,a и посмотрим, что произойдет.

Чтобы суть дела была ясна, вообразим, что место, служащее рынком для обмена всех товаров (А), (В), (С), (D)... между собой, поделено на столько частей, сколько происходит операций обмена товаров друг на друга попарно, т.е. на m(m—1)/2 специальных рынков, обозначаемых табличками с указанием обмениваемых товаров и цен обмена, определяемых математически в соответствии с данной выше системой уравнений. Имеем: «Обмен (А) на (В) и (В) на (А) по взаимным ценам p_a,b, p_b,a»; — «Обмен (А) на (С) и (С) на (А) по взаимным ценам p_a,c, p_c,a»; — «Обмен (В) на (С) и (С) на (В) по взаимным ценам p_b,c, p_c,b». Итак, если бы каждый держатель (А), желающий получить (В) и (С), ограничился обменом своего товара (А) на (В) и (С) на двух первых специальных рынках, если бы каждый держатель (В), желающий получить (А) и (С), ограничился обменом своего товара (В) на (А) и (С) на первом и третьем рынках, если бы каждый держатель (С), желающий получить (А) и (В), ограничился обменом своего товара (С) на (А) и (В) на двух последних рынках, то равновесие сохранилось бы в том виде, как есть. Но нетрудно показать, что ни держатели (А), ни держатели (В), ни держатели (С) не примут этого способа обмена; все они будут действовать иным способом, более для них выгодным.

112. Итак, предположим


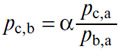
или


где вначале а>1.

Из этого уравнения следует, что настоящая цена (С) в (В) не p_c,b, а p_c,b/α, имея в виду, что c p_c,b/α (В) имеем p_c,bp_b,a/α товара (А) по цене p_a,b=1/p_b,a (А) в (В) на рынке (А,В); и что c p_c,bp_b,a/α (А) имеем p_c,bp_b,ap_a,c/α=1 (С) по цене p_c,a= 1/p_a,c (С) в (А) на рынке (А,С).

Отсюда следует также, что настоящая цена (В) в (А) не p_b,a, а р_b,a/α, имея в виду, что c p_b,a/α (А) имеем p_b,ap_a,c/α товара (С) по цене p_c,a=1/p_a,c (С) в (А) на рынке (А,С); и что c p_b,ap_a,c/α (С) имеем p_b,ap_a,cp_c,b/α=1 (В) по цене p_b,c=1/p_c,b (В) в (С) на рынке (В,С).

Из этого же уравнения, наконец, следует, что настоящая цена (А) в (С) не р_а,с, а р_а,с/α , имея в виду, что c p_a,c/α (С) имеем p_a,cp_c,b/α товара (В) по цене p_b,c=1/p_c,b (В) в (С) на рынке (В,С); и что c p_a,cp_c,b/α (В) имеем p_a,cp_c,bp_b,a/α=1 (А) по цене p_a,b=1/p_b,a (А) в (В) на рынке (А,В).

113. Чтобы закончить выяснение данного пункта с помощью конкретных чисел, предположим, что p_c,b=4, p_c,a=6, p_b,a=2; что дает a=1,33. Из уравнения


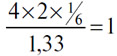
следует, что настоящая цена (С) в (В) не 4, а 4/1,33=3, имея в виду, что c 3 (В) имеем 3х2=6 (А) по цене 1/2 (А) в (В) на рынке (А,В); и что с 6 (A) имеем 6х1/6=1 (С) по цене 6 (С) в (А) на рынке (А,С).

Из уравнения также следует, что настоящая цена (В) в (А) не 2, а 2/1,33=1,50, имея в виду, что с 1,50 (А) имеем 1,50х1/6=1/4 (С) по цене 6 (С) в (А) на рынке (А,С); и что с 1/4 (С) имеем 1/4х4=1 (В) по цене 1/4 (В) в (С) на рынке (В,С).

Из уравнения, наконец, следует, что настоящая цена (А) в (С) не 1/6, а 1/6х1,33=1/8, имея в виду, что с 1/8 (С) имеем 1/8х4=1/2 (В) по цене 1/4 (В) в (С) на рынке (В,С); и что с 1/2 (В) имеем 1/2х2=1 (А) по цене 1/2 (А) в (В) на рынке (А,В).

114. Держатели (А), (В), (С), разумеется, без колебаний проведут следующие замены: одни произведут косвенный обмен (А) на (С) и (С) на (B) вместо прямого обмена (А) на (В); другие — косвенный обмен (В) на (А) и (А) на (С) вместо прямого обмена (В) на (С); третьи — косвенный обмен (С) на (В) и (В) на (А) вместо прямого обмена (С) на (А). Этот косвенный обмен называется арбитражем (арбитражной операцией. — Прим. перев.). Что касается экономии, получаемой таким путем, то они распределят ее по собственному усмотрению на свои потребности, обеспечивая себе дополнительное количество того или иного товара с тем, чтобы получить как можно большую сумму удовлетворения. Мы могли бы указать на условие этого максимума, состоящее в том, чтобы соотношения интенсивностей последних удовлетворенных потребностей были бы равны реальным ценам, проистекающим из арбитражных операций. Но, не входя в данное соображение, достаточно заметить, что этот дополнительный спрос будет предъявляться так же, как и основной: держателями (А) — через обмен (А) на (С) и (С) на (В), но никак не через обмен (А) на (В); держателями (В) — через обмен (В) на (А) и (А) на (С), но никак не через обмен (В) на (С); держателями (С) — через обмен (С) на (В) и (В) на (А), но никак не через обмен (С) на (А). Таким образом, на рынке (А,В) постоянно будет спрос на (А) и предложение (В), но не будет спроса на (В) и предложения (А); отсюда — понижение p_b,a. На рынке (А,С) постоянно будет спрос на (С) и предложение (А), но не будет спроса на (А) и предложения (С); отсюда — повышение p_c,a. На рынке (В,С) постоянно будет спрос на (В) и предложение (С), но не будет спроса на (С) и предложения (В); отсюда — понижение p_c,b.

115. Мы видим тем самым, что в случае, когда p_c,b>p_c,a/p_b,a, равновесие рынка не является окончательным или общим и что на нем происходят арбитражные операции, результат которых — понижение p_c,b, повышение p_c,a и понижение p_b,a. Мы видим в то же самое время, что в случае, когда p_c,bc,a/p_b,a, на рынке пройдут арбитражные операции, результатом которых будет повышение p_c,b, понижение p_c,a и повышение p_b,a. Действительно, тогда мы получим

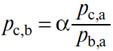
или

где α<1; отсюда вытекает, что настоящая цена (В) в (С) есть αp_b,c при условии обмена (С) на (А) и (А) на (В), что настоящая цена (А) в (В) есть αp_a,b при условии обмена (В) на (С) и (С) на (А), что настоящая цена (С) в (А) есть αp_c,a при условии обмена (А) на (В) и (В) на (С). Впрочем, достаточно очевидно, что то, что было сказано относительно цен (А), (В) и (С), может быть сказано и о ценах любых трех товаров. Если бы, следовательно, мы захотели, чтобы арбитражные операции не имели места, а равновесие товаров, взятых на рынке попарно, было бы общим, то надо было бы ввести условие, по которому цена двух каких-либо товаров, одного в другом, была бы равна отношению цен того и другого к какому-либо третьему товару, т.е. надо было бы сформулировать следующие уравнения:

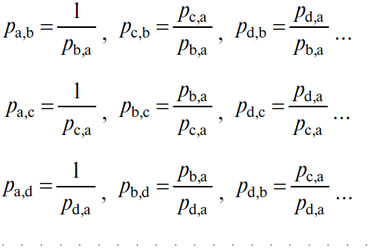
и так далее, или, в целом, (m—1)( m—1) уравнений общего равновесия, содержащих в неявном виде m( m—1)/2 уравнений цен.

Товар, в котором формулируются таким образом цены всех остальных товаров, является счетным.

116. Очевидно, что введение (m—1)( m—1) уравнений, определяющих условие, требует, чтобы наша предыдущая система уравнений спроса и предложения была сокращена на соответствующее число уравнений. Именно это как раз и происходит при замене отдельных рынков на общий рынок при замене уравнений обмена, указывающих на равенство спроса и предложения по каждому товару на каждый из остальных товаров на нижеследующие уравнения обмена, устанавливающие равенство спроса и предложения по каждому товару на все остальные:

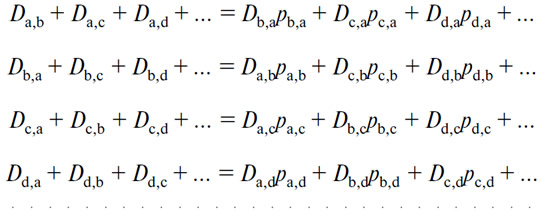
и так далее, итого m уравнений. Но эти m уравнений сокращаются до m—1. Действительно, если ввести в них значения цен, выведенные из уравнений общего равновесия, и обозначить просто через p_b, p_c, p_d... цены (В), (С), (D). в (А), то они примут вид

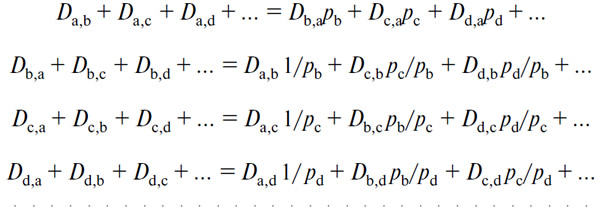
И если теперь мы сложим вместе последние m—1, умножив предварительно обе части первого уравнения на p_b, второго — на p_c, третьего — на p_d..., и вычтем из той и другой части тождественные члены, то мы вернемся к первому уравнению системы. Этим первым уравнением можно, следовательно, пренебречь, и система сокращается до m—1 последующих уравнений. Эти уравнения остаются как m—1 уравнений обмена, которые вместе с m (m—1) уравнениями спроса и (m—1)( m—1) уравнениями общего равновесия образуют совокупность в 2 m(m—1) уравнений, корнями которых являются m (m—1) цен m товаров, выраженных в ценах других, и m (m—1) совокупных количеств данных m товаров, обмененных друг на друга. Вот как математически выводятся цены, если даны уравнения спроса. Остается только показать — и это основной пункт, — что эта же самая проблема обмена, чье теоретическое решение мы только что дали, является также проблемой, которая практически решается на рынке через механизм свободной конкуренции. Однако прежде чем приступить к этому доказательству, мы рассмотрим случай, когда обменивающиеся лица являются держателями нескольких товаров, что представляет собой общий случай, который теорема максимального удовлетворения позволяет разобрать простым и доступным образом.

Источник: «Элементы чистой политической экономии», Л. Вальрас, М.: Изограф, 2000