Решение уравнений производства. Закон установления цен на продукты и услуги

Содержание:

• 208. Гипотеза о предпринимателях, покупающих, и о потребителях, продающих производительные услуги в эквивалентных количествах. Цены на производительные услуги, объявляемые наугад.
• 209. Себестоимость продуктов. Количества продуктов, изготовляемые наугад.
• 210. Продажная цена продуктов. Прибыли или убытки предпринимателей.
• 211, 212. «Нащупывание» с целью нахождения равенства продажной цены и себестоимости продуктов.
• 213. Спрос на счетный продукт. Необходимость равенства себестоимости счетного продукта единице для установления равновесия производства.
• 214. Гипотеза о предпринимателях, покупающих, и потребителях, продающих производительные услуги в равных количествах.
• 215. Действительные спрос и предложение услуг. Количества, запрашиваемые предпринимателями; количества, запрашиваемые потребителями. Изменения спроса и предложения в зависимости от изменения цены от нуля до бесконечности.
• 216, 217. Нащупывание с целью нахождения равенства предложения и спроса на услуги.
• 218. Спрос на счетный продукт.
• 219. Нащупывание с целью нахождения равенства себестоимости счетного продукта единице.
• 220. Закон установления равновесных цен на продукты и услуги.

208. Итак, давайте пойдем на рынок и предположим, что здесь определяют наугад n цен на услуги p'_t, p'_p, p'_k... и m количеств продуктов, подлежащих изготовлению, Ω_a, Ω_b, Ω_c, Ω_d..., представленных талонами. Чтобы лучше понять суть операций, которые последуют ниже, мы предположим сначала, что предприниматели продают, а потребители покупают определенные количества продуктов (А), (В), (С), (D)..., при этом первые покупают, а вторые продают не равные, а просто эквивалентные количества производительных услуг (Т), (Р), (К)..., и мы определим тем самым Ω_a, Ω_b, Ω_c, Ω_d... так, чтобы предприниматели не имели ни прибыли, ни убытков. Затем мы примем предположение, что предприниматели покупают, а потребители продают не только эквивалентные, но и равные количества производительных услуг, и определим тем самым p'_t, p'_p, p'_k... так, чтобы действительные предложение и спрос были равны. Нетрудно видеть, что при такой манере изложения мы абстрагируемся если и не от счетного товара, то, по меньшей мере, от денег.


Может быть, небесполезно заметить, что в принимаемых нами данных и условиях задачи мы предполагаем, что собственно капиталы арендуются в натуре. Тем не менее мы ранее объясняли (§ 190), что в реальности капиталы арендуются в денежной форме в силу того, что капиталист так формировал свой капитал путем сбережений. Но создание капиталов и одновременно их аренду в форме денег мы рассмотрим позже.

209. Если цены p'_t, p'_p, p'_k... на (Т), (Р), (К). определяются, как мы говорили, наугад, то отсюда следуют — для предпринимателей — определенные себестоимости p'_a, p'_b, p'_c, p'_d... в соответствии с уравнениями


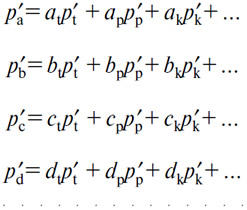
Мы были бы вольны, отметим это особо, определить p'_t, p'_p, p'_k... так, чтобы иметь p'_a= 1. Мы воспользуемся этой возможностью в свое время и в своем месте, впрочем, ниже мы покажем, что себестоимость счетного товара при режиме свободной конкуренции сама стремится к равенству с единицей. А пока мы будем рассуждать так, как если бы себестоимость (А) могла бы быть как больше или меньше своей продажной цены, так и равной ей.

Впрочем, количества Ω_a, Ω_b, Ω_c, Ω_d... продуктов (А), (В), (С), (D)..., также определяемые наугад, требуют количеств Δ_t, Δ_p, Δ_k... (Т), (Р), (К). в соответствии с уравнениями


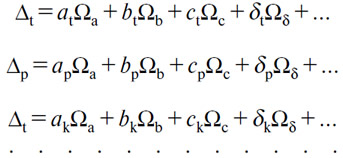
Эти количества Ω_a, Ω_b, Ω_c, Ω_d... будут проданы предпринимателями в соответствии с механизмом свободной конкуренции. Исследуем сначала условия продажи продуктов (В), (С), (D)... Затем мы рассмотрим условия продажи продукта (А), служащего счетным товаром.


210. Количества Ω_b, Ω_c, Ω_d... (В), (С), (D)... будут продаваться по продажным ценам p_b, p_c, p_d... в соответствии с уравнениями


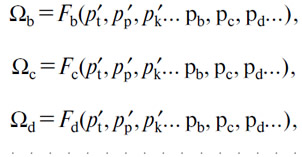
Действительно, поскольку рынок управляется свободной конкуренцией, то продукты продаются на нем при тройном условии: 1) максимального удовлетворения потребностей; 2) единственности цен как продуктов, так и услуг; 3) общего равновесия (§ 124). А предыдущая система — это система из m—1 уравнений с m—1 неизвестными, которая в точности отвечает этим трем условиям.

Итак, поскольку продажные цены p_b, p_c, p_d... обычно отличаются от себестоимостей p'_b, p'_c, p'_d..., то предприниматели, имеющие (В), (С), (D)..., получат прибыли или понесут убытки, выражаемые разностями


Но мы сразу же видим, что, если Ω_b, Ω_c, Ω_d... есть функции от π_b, π_с, π_d..., то эти последние количества являются — в силу того же факта — функциями от первых и что, следовательно, изменяя должным образом количества (В), (С), (D)..., подлежащие изготовлению, мы можем сделать так, чтобы продажные цены этих продуктов согласовывались с их себестоимостью.

211. Нам неизвестны функции F_b, F_c, F_d..., но из самой природы факта обмена следует, однако, что эти функции являются возрастающими либо убывающими при убывающих либо возрастающих значениях: p_b — для первой, р_с — для второй, р_d — для третьей и т. д. Таким образом, если предположить, например, что π_b>p_b, то можно уменьшить π_b, увеличивая Ω_b; а если предположить, напротив, что π_bb, то можно увеличить π_b, уменьшая Ω_b. Равным образом, если μ_c<>p'_c, π_d<>p'_d, то можно уменьшать или увеличивать p_c, p_d..., увеличивая или уменьшая Ω_c, Ω_d.

Пусть Ω_b, Ω_c, Ω_d... — подлежащие изготовлению количества (В), (С), (D)., для которых мы имеем

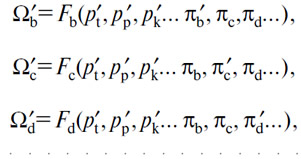
Эти количества, которые заменят в ходе нащупывания количества Ω_b, Ω_c, Ω_d..., будут продаваться — в соответствии с механизмом свободной конкуренции — по ценам p'_b, p'_c, p'_d... согласно уравнениям

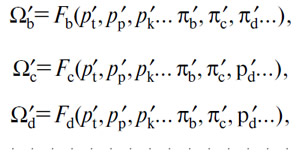
и необходимо установить, являются ли значения π'_b, π'_c, π'_d... более близкими к равенству с p'_b, p'_c, p'_d... , чем были ранее π_b, π_c, π_d.

212. В условиях нащупывания, проводимого нами в данный момент, цены услуг постоянны и не изменяются. Следовательно, каждое обменивающееся лицо имеет все тот же доход, оцениваемый в счетном товаре

и должно распределить этот доход между потреблением услуг и потреблением продуктов согласно уравнению

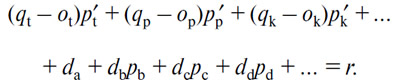
После того как на (В), (С), (D). установились определенные цены вслед за изготовлением определенных количеств этих товаров и одно из произведенных количеств, например количество (В), увеличилось или уменьшилось, то первое, что нужно сделать — для восстановления нового равновесия — это расширить или же сократить спрос на (В) со стороны всех обменивающихся лиц с тем, чтобы уменьшить или увеличить редкости в общей и идентичной пропорции и снизить либо повысить в то же самое время цену (В) в той же пропорции. Это можно назвать следствием первого порядка, имеющим существенное значение в том, что касается цены (В). Если это сделано, то равновесие будет восстановлено, если для каждого обменивающегося лица сумма, идущая на потребление (В), d_bp_b, не изменилась. Но поскольку эта сумма — по всей видимости и в любом случае, т.е. либо в случае увеличения, либо в случае уменьшения произведенного количества (В) — возрастет для одних и сократится для других, то первые должны будут продавать некоторое количество всех товаров, что будет вести к понижению цен, а другие — покупать их, что должно вести к повышению цен. В этом будет состоять последствие второго порядка, имеющее несущественное значение в том, что касается цен (В), (С), (D)..., по следующей тройной причине: 1) изменение суммы, идущей на потребление (В), d_bp_b, ограничено в силу того, что оба фактора d_b и p_b изменяются в обратном направлении, 2) данное изменение, влекущее за собой продажу и покупку некоторого количества всех товаров, вызывает тем самым продажу и покупку лишь крайне малого количества каждого из них, 3) последствия продажи и последствия покупки сталкиваются друг с другом.

То, что только что было сказано о последствиях изменения производимого количества (В), можно было бы сказать и о последствиях изменения производимых количеств (С), (D)... Итак, очевидно, что изменение произведенного количества каждого продукта произвело на продажную цену этого продукта прямое действие, полностью идущее в одном направлении, в то время как изменения произведенных количеств остальных продуктов, если предположить, что они прошли в том же направлении, оказали на эту продажную цену лишь косвенные воздействия, причем одни из них противоположны другим и до известной степени одни компенсируют другие. Система новых произведенных количеств и новых продажных цен находится, следовательно, ближе к равновесию, чем прежняя система, и необходимо только продолжать нащупывание, чтобы все больше и больше приближаться к нему.

Таким образом мы придем к определению некоторых количеств D'_b, D'_c, D'_d... (B), (С), (D)..., требующих количеств D'_t, D'_p, D'_k... (T), (P), (K)... в соответствии с уравнениями

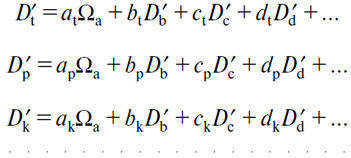
продающихся по продажным ценам p'_b, p'_b, p'_d... в соответствии с уравнениями

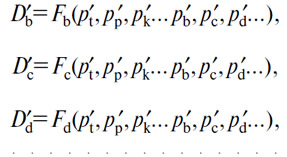
и при которых предприниматели, производящие (B), (С), (D)..., не будут иметь ни прибыли, ни убытков.

Но это нащупывание и есть как раз то самое, которое делается само собой на рынке продуктов при режиме свободной конкуренции, когда предприниматели расширяют свое производство или же ограничивают его в зависимости от того, получают ли они прибыль либо терпят убытки (§ 188).

213. При продажных ценах, равных себестоимостям p'_b, p'_c, p'_d..., на рынке страны действительно запрашиваемым количествам D'_b, D'_c, D'_d... (B), (С), (D)... соответствуют действительно предлагаемые количества в форме талонов O'_t, O'_p, O'_k. (Т), (Р), (К). в соответствии с уравнениями полного предложения услуг

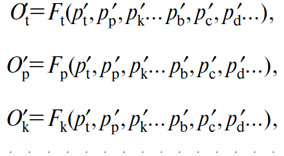
которые вместе с уравнениями полного спроса на продукты образуют систему уравнений обмена, отвечающую трем условиям максимального удовлетворения, единственности цен и общего равновесия.

И тогда также предъявляется действительный спрос на количество D'_a(A), определяемое уравнением

Впрочем, из двух систем уравнений, из которых одна дает себестоимости продуктов как функцию от цен на производительные услуги (§ 209), а вторая — запрашиваемые количества производительных услуг как функцию от произведенных количеств продуктов (§ 212), перемножая m уравнений первой системы соответственно на Ω_a, D'_b, D'_c, D'_d... и n уравнений второй соответственно на p'_t, p'_p, p'_k..., складывая обе полученные таким образом системы и замечая, что правые части обеих сумм тождественны, получаем

Следовательно, мы также имеем

Произведенное количество счетного товара (А) пока определено только наугад; но и его следует определить так, чтобы предприниматели не имели ни прибыли, ни убытков. Но для этого, естественно, необходимо, чтобы себестоимость счетного товара была равна его продажной цене. Именно это и будет иметь место, если мы позаботимся о том, чтобы сначала сформулировать

Вне этого уравнения равновесие невозможно. А если предположить, что оно удовлетворено, то равновесие будет иметь место, когда будут определены D'_b, D'_c, D'_d..., как это было сказано выше. Действительно, количества производительных услуг, которые предприниматели взяли в долг, и количества, которые они должны получить в обмен на свои продукты, будут эквивалентны, поскольку, если р'_a равно 1, предприниматели (А), как и предприниматели (В), (С), (D)..., не будут иметь ни прибыли, ни убытков. Таким образом, мы получим

и, следовательно, также

Таким образом, практически, после того как будут определены цены услуг так, чтобы себестоимость счетного продукта была равна единице, то — для достижения искомого нами частичного равновесия — будет достаточно, как мы говорили, определить D'_b, D'_c, D'_d… так, чтобы предприниматели (В), (С), (D). не имели ни прибыли, ни убытков. Запрашиваемое количество (А), D'_a , будет, естественно, произведенным наугад количеством Ω_a.

И тогда, поскольку производители продают с помощью талонов продукты на сумму D'_a + D'_bp'_b + D'_cp'_c + D'_dp'_d..., с тем, чтобы купить услуги на сумму D'_tp'_t + D'_pp'_p + D'_kp'_k..., а потребители продают с помощью талонов услуги на сумму O'_tp'_t + O'_pp'_p + O'_kp'_k..., чтобы купить продукты на сумму D'_a + D'_bp'_b + D'_cp'_c + D'_dp'_d..., будут удовлетворяться все уравнения производства, исключая систему [3] равенства применяемых количеств производительных услуг и предлагаемых количеств.

214. Но и эта система, как и остальные, должна удовлетворяться. Необходимо, чтобы купленные и проданные количества производительных услуг были не только эквивалентны, но и равны, поскольку именно эти самые количества должны вступить в процесс изготовления продуктов. Таким образом, наступил момент закрыть, так сказать, круг производства, подойдя к равенству предложения услуг и спроса на них.

Это равенство имело бы место, если бы у нас D'_t=O'_t, D'_p=O'_p, D'_k=O'_k... Тогда агенты (маклеры) рынков передали бы производителям талоны на услуги взамен талонов на продукты, а потребителям — талоны на продукты взамен талонов на услуги, и произошел бы обмен услуг на продукты и услуг на услуги. Но в общем случае мы получим D'_t<>O'_t, D'_p<>O'_p, D'_k<>O'_k... И надо возобновить нащупывание на основе рационально изменяемых цен услуг. Заметим, что, поскольку p'_t, p'_p, p'_k. по существу положительны, когда мы делаем р'_a=1 и получаем Ω_a=D'_a, то среди количеств O'_t - D'_t, O'_p - D'_p, O'_k - D'_k. некоторые количества положительны, а другие отрицательны, и наоборот.

215. Функцию O'_t можно поставить в виде U—u, где U выражает сумму положительных о_t, т.е. действительно предложенные количества услуги (Т), а функция и — сумму отрицательных о_t, т.е. действительно запрошенные количества этой услуги, но не предпринимателями для производства (А), (В), (С), (D)..., а потребителями в качестве товара, т.е. не как производительная услуга, а как услуга потребляемая. Таким образом, неравенство D'_t<>O'_t можно поставить в виде

Предположим, что D'_a не изменяется, т.е. что предприниматели (А) производят этот продукт все время в том же количестве, какими бы ни были изменения (колебания) p_t, p_p, p_k... и, следовательно, себестоимости pa. В первой части остаются: переменные члены b_tD'_b, c_tD'_c, d_tD'_d..., являющиеся убывающими функциями цен p_b, p_c, p_d... и, следовательно, цены p_t, себестоимости которой сами являются возрастающими функциями, и переменный член u, который также является убывающей функцией от цены pt. Таким образом, если p_t возрастает от нуля до бесконечности, а p'_p, p'_k... остаются постоянными, то D'_t+u будет уменьшаться начиная с некоторого определенного значения до нуля.

Что касается единственного члена второй части неравенства, U, то он равен нулю при нулевом значении и даже при некоторых положительных значениях p_t. Это тот случай, когда стоимости различных продуктов по отношению к стоимости услуги (Т) достаточно высоки, в результате чего спрос на эти продукты со стороны владельцев этой услуги равен нулю. Когда цена p_t растет, то функция U сначала растет. Так как продукты в этом случае становятся менее дорогими по отношению к услуге (Т), то спрос на эти продукты имеет место одновременно с предложением сопровождающей его услуги. Но это предложение не возрастает бесконечно. Оно проходит, по меньшей мере, через один максимум, который не может быть больше полного имеющегося количества Q_t; затем оно уменьшается и вновь становится нулевым, если цена (Т) становится бесконечной, т.е. если (А), (В), (С), (D)... бесплатны. Таким образом, если p_t возрастает от нуля до бесконечности, U начинает с нуля, возрастает, затем уменьшается и возвращается к нулю.

216. В этих условиях, если только D'_t+u не становится равным нулю до того, как U перестало быть нулевым, случай, когда решения нет, имеется определенное значение p_t, которое <>p_t в зависимости от того, что D'_t+u<>U, при котором действительные предложение и спрос на (Т) равны. Пусть p''_t есть это значение; пусть π_b, π_c, π_d... продажные цены, равные себестоимостям (В), (С), (D)..., получаемые так, как это говорилось выше; пусть Ω''_t — соответствующее предложение (Т), равное спросу, в этом случае имеем

После того как эта операция выполнена, функция

принимает вид

и это предложение услуги (Р) является большим или меньшим, чем спрос на нее. Но имеется некоторое значениеp при котором действительные предложение и спрос на (Р) равны и которое можно найти тем же способом, что и p''_t. Пусть p''_p есть это значение; пусть π'''_b, π'''_c, π'''_d... — продажные цены, равные себестоимостям (В), (С), (D)..., получаемые так, как это говорилось выше (§§ 211, 212); пусть Ω'''_p — соответствующее предложение (Р), равное спросу, в этом случае имеем

Аналогично получаем

и так далее.

217. После того как все эти операции выполнения, имеем

и необходимо установить, что это предложение O''_t ближе к равенству со спросом D''_t, чем были предложение O'_t и спрос D'_t. Но это представляется вероятным, если учесть, что изменение p'_t в p''_t, которое привело предложение и спрос к равенству, имело прямой эффект и, по крайней мере, в том, что касается спроса на (Т), полностью идущий в одном направлении, в то время как изменения p'_p, p'_k... в p''_p, p''_k..., которые удалили это предложение и этот спрос от равенства, имели косвенный эффект и, по крайней мере, в том, что касается спроса на (Т), в противоположном направлении, до известной степени компенсируя друг друга. Система новых цен p''_t, p''_p, p''_k... находится, следовательно, ближе к равновесию, чем система старых цен p'_t, p'_p, p'_k..., и необходимо только продолжать следовать тому же методу, чтобы все больше и больше приближаться к нему.

Но на рынке услуг при режиме свободной конкуренции это нащупывание происходит естественным образом, поскольку при таком режиме цену услуг повышают, когда спрос больше предложения, и понижают, когда предложение больше спроса.

218. Предположим, что мы пришли к равновесию и имеем следующие цены продуктов

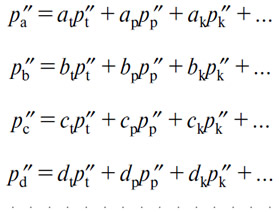
и, с другой стороны, имеем запрашиваемые количества производительных услуг

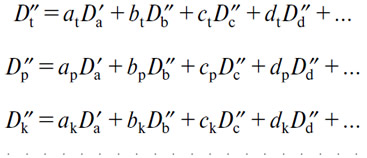
впрочем, количества D''_b, D''_c, D''_d. удовлетворяют уравнениям спроса на продукты (В), (С), (D)..., а количества D''_t=О''_t, D''_p=O''_p , D''_k=O''_k... — уравнениям предложения услуг (Т), (Р), (К)., в которых p''_t, p''_p, p''_k... p''_b, p''_c, р''_d - являются независимыми переменными. Из двух вышеуказанных систем выводим уравнение

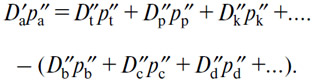
В этом случае предъявляется спрос на количество D''_a (А) согласно уравнению

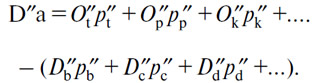
Поскольку D''_t=O''_t, D''_p=O''_p, D''_k=O''_k..., получаем

Откуда видно, что мы удовлетворили всем уравнениям задачи, исключая уравнение себестоимости счетного товара, которое дало бы равенство предложения и спроса, или уравнение спроса на этот самый счетный товар, которое дало бы равенство продажной цены себестоимости, т.е. единице. Таким образом, если бы мы случайно получили p''_a=1, то мы также получили бы D''_a=D'_a, или же, если бы мы случайно получили D''_a=D'_a, то мы имели бы также p''_a=1, и задача была бы полностью решена. Но обычно после изменений p'_t, p'_p, p'_k... в p''_t, p''_p, p''_k..., проведенных так, как сказано выше, мы получим

и, следовательно,

219. Чтобы закончить решение системы уравнений производства, нам надо еще раз провести весь процесс нащупывания, определяя p'''_t, p'''_p, p'''_k. согласно уравнению

т.е. делая p'''_t<>p''_t, p'''_p<>p''_p, p'''_k<>p''_k... в зависимости от p''_a<>1.

Исходя из этой новой точки, мы придем сначала — в ходе первой фазы на рынке продуктов — к определению D'''_a согласно уравнению

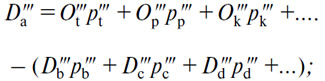
а затем — в ходе второй фазы на рынке услуг — к определению D_a^IV согласно уравнению

и необходимо установить, что p^IV_a ближе к единице, чем была p''_a. Но это представляется вероятным, если подумать, что, например, в случае, когда p" была > 1, мы получали p'''_bb, p'''_cc, p'''_dd... и, как следствие, D'''_b>D''_b, D'''_c>D''_c, D'''_d>D''_d. и, также как следствие, D'''_aa. Таким образом, чтобы превратиться в p_a^IV, p'''_a=1 возросло путем увеличения спроса на (В), (С), (D)... и снизилось путем уменьшения спроса на (А). В случае, если p''_a была бы < 1, то, чтобы превратиться в p_a^IV, p'''_a снизилась бы путем уменьшения спроса на (В), (С), (D). и возросла бы путем увеличения спроса на (А). Как в одном, так и в другом случае, поскольку эти тенденции противоположны, p_a стала бы, вероятно, менее удаленной от единицы в силу их последствий по сравнению с приближением к единице в результате снижения или возрастания p_t, p_p, p_k... И, продолжая следовать тому же самому методу, мы будем все больше приближать ее к единице. Предположим, что это произошло и что мы имеем p^IV_a=1, тогда мы имеем также D'''_a=D^IV_a, и задача полностью решена.

Но ведь нащупывание, которое мы только что описали, совершается при режиме свободной конкуренции естественным образом. Действительно, когда мы имеем

то производители (А) должны D'_ap''_a. И если они отдают в этом случае запрашиваемое количество (А) по цене 1, D''_a, они имеют в качестве прибыли D'_a—D''_a=D'_a(1—р''_a). Эта разница есть прибыль в собственном смысле слова, если р''_a<1 и D'_a>D''_a. Но в этом случае они развивают свое производство, приводят к увеличению p''_t, p''_p, p''_k..., и, следовательно, р''_a приближается к единице. Разница будет убытком, если р''_a>1 и D'_aa. У производителей остался бы долг в размере этого убытка D''_a—D'_a Но тогда они бы сократили свое производство, привели к уменьшению p''_t, p''_p, p''_k..., и, следовательно, р''_a приблизилось бы к единице. Следует заметить, что предприниматели (А) вольны избегать такой ситуации, не производя, когда себестоимость счетного товара больше его продажной цены, т.е. единицы, и заведомо приносит им убыток, а производя только тогда, когда себестоимость ниже или равна единице. Как бы там ни было, в конечном счете предпринимателям (А), равно как и предпринимателям (В), (С), (D)..., следует развивать, как это они и делают, свое производство в случае превышения продажной цены над себестоимостью и ограничивать его в случае превышения себестоимости над продажной ценой. В первом случае они повышают цену услуг, во втором — понижают ее на рынке услуг. В обоих случаях их действия направлены на установление равновесия.

220. Объединяя все части данного доказательства, мы приходим к формулированию закона установления текущих или равновесных цен производства следующим образом: — Если дано некоторое число услуг, с помощью которых можно изготовить разные продукты, и обмен которых на продукты совершается с участием счетного товара, то, чтобы имелось рыночное равновесие или стационарные цены на все эти услуги и все эти продукты в счетном товаре, необходимо и достаточно: 1) чтобы при этих ценах действительный спрос на каждую услугу и на каждый товар был равен его действительному предложению; 2) чтобы продажная цена продуктов была равна их себестоимости в услугах. Если этого двойного равенства нет, необходимо — чтобы прийти к первому равенству — повышение цены услуг или продуктов, действительный спрос на которые больше действительного предложения, и понижение цены тех (услуг и продуктов), чье действительное предложение больше действительного спроса; а чтобы прийти ко второму равенству — увеличение количества продуктов, чья продажная цена выше себестоимости, и уменьшение количества тех (продуктов), чья себестоимость выше продажной цены.

Таков закон установления равновесных цен производства; если объединить с ним (что мы сейчас и сделаем) закон изменения равновесных цен, обобщенный должным образом, то мы получим научную формулировку двойного закона предложения и спроса и себестоимости.

Источник: «Элементы чистой политической экономии», Л. Вальрас, М.: Изограф, 2000